题目内容
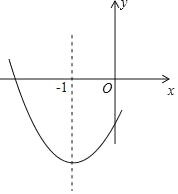
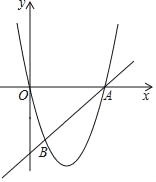
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
【答案】(1)y=x2﹣6x,y=x﹣6;(2)C(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)利用待定系数法求二次函数和一次函数的解析式;
(2)先说明OA=OH=6,则∠OAH=45°,作辅助线,根据正切值证明∠BOC=∠OBE,作OB的垂直平分线交AB于C,交OB于F,解法一:先根据中点坐标公式可得F(![]() ),易得直线OB的解析式为:y=﹣5x,根据两直线垂直的关系可得直线FC的解析式为:y
),易得直线OB的解析式为:y=﹣5x,根据两直线垂直的关系可得直线FC的解析式为:y![]() ,列方程
,列方程![]() x﹣6,解出可得C的坐标;
x﹣6,解出可得C的坐标;
解法二:过C作CD⊥x轴于D,连接OC,设C(m,m﹣6),根据OC=BC,列方程可得结论.
(1)把点A(6,0)和点B(1,﹣5)代入抛物线y=ax2+bx得:
![]() ,解得:
,解得:![]() ,∴这条抛物线的表达式:y=x2﹣6x,设直线AB的解析式为:y=kx+b,把点A(6,0)和点B(1,﹣5)代入得:
,∴这条抛物线的表达式:y=x2﹣6x,设直线AB的解析式为:y=kx+b,把点A(6,0)和点B(1,﹣5)代入得:![]() ,解得:
,解得:![]() ,则直线AB的解析式为:y=x﹣6;
,则直线AB的解析式为:y=x﹣6;
(2)当x=0时,y=6,当y=0时,x=6,∴OA=OH=6.
∵∠AOH=90°,∴∠OAH=45°,过B作BG⊥x轴于G,则△ABG是等腰直角三角形,∴AB=5![]() ,过O作OE⊥AB于E,S△AOH
,过O作OE⊥AB于E,S△AOH![]() AHOE
AHOE![]() OAOH,6
OAOH,6![]() OE=6×6,OE=3
OE=6×6,OE=3![]() ,∴BE=AB﹣AE=5
,∴BE=AB﹣AE=5![]() ,Rt△BOE中,tan∠OBE
,Rt△BOE中,tan∠OBE![]() .
.
∵∠BOC的正切值是![]() ,∴∠BOC=∠OBE,∴OC=CB.作OB的垂直平分线交AB于C,交OB于F,解法一:∵B(1,﹣5),∴F(
,∴∠BOC=∠OBE,∴OC=CB.作OB的垂直平分线交AB于C,交OB于F,解法一:∵B(1,﹣5),∴F(![]() ),易得直线OB的解析式为:y=﹣5x,设直线FC的解析式为:y
),易得直线OB的解析式为:y=﹣5x,设直线FC的解析式为:y![]() x+b,把F(
x+b,把F(![]() )代入得:
)代入得:![]() b,b
b,b![]() ,∴直线FC的解析式为:y
,∴直线FC的解析式为:y![]() x﹣6,x
x﹣6,x![]() ,当x
,当x![]() 时,y
时,y![]() ,∴C(
,∴C(![]() );
);
解法二:过C作CD⊥x轴于D,连接OC,设C(m,m﹣6),则AC![]() (6﹣m).
(6﹣m).
∵OC=BC,∴m2+(m﹣6)2=[5![]() (6﹣m)],m
(6﹣m)],m![]() ,∴C(
,∴C(![]() ).
).

 科学实验活动册系列答案
科学实验活动册系列答案【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.