题目内容
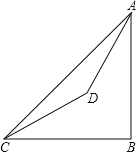
【题目】已知:如图,在山脚的![]() 处测得山顶
处测得山顶![]() 的仰角为
的仰角为![]() ,沿着坡度为
,沿着坡度为![]() 的斜坡前进
的斜坡前进![]() 米到
米到![]() 处(即
处(即![]() ,
,![]() 米),测得
米),测得![]() 的仰角为
的仰角为![]() ,求此山的高度
,求此山的高度![]() .(答案保留根号)
.(答案保留根号)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】此山的高度![]() 为
为![]() 米
米
【解析】
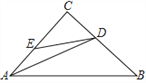
首先根据题意分析图形,作DE⊥AB于E,作DF⊥BC于F,构造两个直角三角形,分别求解可得DF与AE的值,再利用图形关系,进而可求出答案.
解答:如图,作DE⊥AB于E,作DF⊥BC于F,
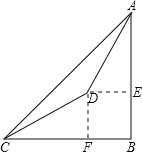
∵在Rt△CDF中,∠DCF=30,CD=400米,
∴DF=CDsin30=![]() ×400=200(米),
×400=200(米),
CF=CDcos30=![]() ×400=200
×400=200![]() (米).
(米).
∵在Rt△ADE中,∠ADE=63,设DE=x米,
∴AE=tan63x=![]() x(米).
x(米).
在矩形DFBE中,BE=DF=200米,
∵在Rt△ACB中,∠ACB=53,
∴tan53=![]() ,即:
,即:![]() =
=![]() ,
,
∴x=250![]()
![]() ,
,
∴AB=AE+BE=![]() (250
(250![]()
![]() )+200=600
)+200=600![]() 250(米).
250(米).
答:此山的高度AB为(600![]() 250)米.
250)米.
故答案为:(600![]() 250)米.
250)米.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目