题目内容
（1）通过观察、计算，探索规律：
32-12=4×2=（3+1）（3-1）
52-22=7×3=（5+2）（5-2）
82-32=11×5=（8+3）（8-3）
72-42=______；
请用你发现的规律填空：a2-b2=______；
（2）观察下面由※组成的图案和算式，解答问题：
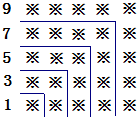1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
①请猜想1+3+5+7+9+…+19=______；
②请猜想1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）=______．
解：（1）72-42=11×3=（7+4）（7-4）；
a2-b2=（a+b）（a-b）；
（2）①1+3+5+7+9+…+19=102；
②1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）=（n+1）2．
故答案为11×3=（7+4）（7-4）；（a+b）（a-b）；102；（n+1）2．
分析：（1）观察几个等式的计算规律得到两个数的平方差等于这两个数的和与差的积，则有a2-b2=（a+b）（a-b）；
（2）观察图形与算式得到从1开始的几个连续奇数的和等于奇数的个数的平方，由于1到19共有10个数，则1+3+5+7+9+…+19=102；从1到2n+3共有n+1个数，则1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）=（n+1）2．
点评：本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．
a2-b2=（a+b）（a-b）；
（2）①1+3+5+7+9+…+19=102；
②1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）=（n+1）2．
故答案为11×3=（7+4）（7-4）；（a+b）（a-b）；102；（n+1）2．
分析：（1）观察几个等式的计算规律得到两个数的平方差等于这两个数的和与差的积，则有a2-b2=（a+b）（a-b）；
（2）观察图形与算式得到从1开始的几个连续奇数的和等于奇数的个数的平方，由于1到19共有10个数，则1+3+5+7+9+…+19=102；从1到2n+3共有n+1个数，则1+3+5+7+9+…+（2n-1）+（2n+1）+（2n+3）=（n+1）2．
点评：本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．
练习册系列答案
智慧小复习系列答案
相关题目
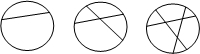如图，一块圆形烙饼切一刀可以切成2块，若切两刀最多可以切成4块，切三刀最多可以切成7块…通过观察、计算填下表（其中S表示切n刀最多可以切成的块数）后，可探究一圆形烙饼切n刀最多能切成
1+3=4=22