题目内容
已知:正方形ABCD的边长为2,△EFG为等腰直角三角形,∠EGF=90°.
(1)如图1,当点G与点D重合,点E在正方形ABCD的对角线AC上时.求AE+AF的值;
(2)如图2,当点G与点D重合,点E在线段CA的延长线上时.通过观察、计算,你能发现AF与AE有怎样的数量关系,并说明理由;
(3)如图3,当点G在线段DA的延长线上时,设AG=x.则线段AE、AF与x有怎样的数量关系,请说明理由.
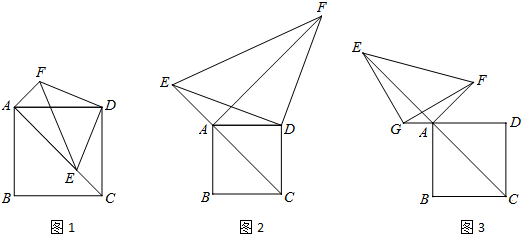
(1)如图1,当点G与点D重合,点E在正方形ABCD的对角线AC上时.求AE+AF的值;
(2)如图2,当点G与点D重合,点E在线段CA的延长线上时.通过观察、计算,你能发现AF与AE有怎样的数量关系,并说明理由;
(3)如图3,当点G在线段DA的延长线上时,设AG=x.则线段AE、AF与x有怎样的数量关系,请说明理由.

分析:(1)当点G与点D重合,点E在正方形ABCD的对角线AC上时,AE+AF=2
,首先利用正方形的性质和等腰直角三角形的性质证明△FDA≌△EDC,由全等的性质得到AF=EC,
再利用勾股定理求出AC=2
,所以AE+AF=AE+EC=AC=2
;
(2)当点G与点D重合,点E在线段CA的延长线上时,AF-AE=2
,首先利用正方形的性质和等腰直角三角形的性质证明△FDA≌△EDC,由全等的性质得到AF=EC,∴AF-AE=EC-AE=AC=2
;
(3)当点G在线段DA的延长线上时,设AG=x,AE-AF=
x,过点G作GH⊥AG,交AE于点H,利用已知条件首先证明△FGA≌△EGH,所以AE-AF=AE-EH=AH,在Rt△GAH中,根据勾股定理得到AH=
=
x,所以AE-AF=
x.
| 2 |
再利用勾股定理求出AC=2
| 2 |
| 2 |
(2)当点G与点D重合,点E在线段CA的延长线上时,AF-AE=2
| 2 |
| 2 |
(3)当点G在线段DA的延长线上时,设AG=x,AE-AF=
| 2 |
| AG2+AH2 |
| 2 |
| 2 |
解答:解:(1)∵四边形ABCD为正方形,
∴AD=CD,∠ADC=90°,
∵△GEF为等腰直角三角形,
∴GF=GE,∠EGF=90°,
∴∠FDA=∠CDE,
∴△FDA≌△EDC(SAS)
∴AF=EC,
∵根据勾股定理:AC=2
∴AE+AF=AE+EC=AC=2
;
(2)AF-AE=2
,
∵四边形ABCD为正方形
∴AD=CD,∠ADC=90°,
∵△GEF为等腰直角三角形,
∴GF=GE,∠EGF=90°,
∴∠FDA=∠CDE,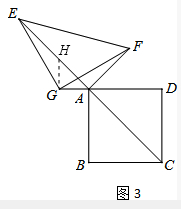
∴△FDA≌△EDC(SAS),
∴AF=EC
∴AF-AE=EC-AE=AC=2
;
(3)AE-AF=
x,
过点G作GH⊥AG,交AE于点H,
∴∠HGA=90°,
∵AC为正方形对角线,
∴∠GAE=45°
∴△GAH为等腰直角三角形,
∴HG=AG,
又∵GF=GE,∠EGF=90°,
∴∠EGH=∠FGA,
∴△FGA≌△EGH(SAS),
∴EH=AF,
∴AE-AF=AE-EH=AH,
在Rt△GAH中,根据勾股定理:
∴AH=
=
x,
∴AE-AF=
x.
∴AD=CD,∠ADC=90°,
∵△GEF为等腰直角三角形,
∴GF=GE,∠EGF=90°,
∴∠FDA=∠CDE,
∴△FDA≌△EDC(SAS)
∴AF=EC,
∵根据勾股定理:AC=2
| 2 |
∴AE+AF=AE+EC=AC=2
| 2 |
(2)AF-AE=2
| 2 |
∵四边形ABCD为正方形
∴AD=CD,∠ADC=90°,
∵△GEF为等腰直角三角形,
∴GF=GE,∠EGF=90°,
∴∠FDA=∠CDE,

∴△FDA≌△EDC(SAS),
∴AF=EC
∴AF-AE=EC-AE=AC=2
| 2 |
(3)AE-AF=
| 2 |
过点G作GH⊥AG,交AE于点H,
∴∠HGA=90°,
∵AC为正方形对角线,
∴∠GAE=45°
∴△GAH为等腰直角三角形,
∴HG=AG,
又∵GF=GE,∠EGF=90°,
∴∠EGH=∠FGA,
∴△FGA≌△EGH(SAS),
∴EH=AF,
∴AE-AF=AE-EH=AH,
在Rt△GAH中,根据勾股定理:
∴AH=
| AG2+AH2 |
| 2 |
∴AE-AF=
| 2 |
点评:本题考查了正方形的性质、等腰三角形的性质和判定、全等三角形的性质和判定以及勾股定理的运用,题目的综合性很强,难度不小,特别是第三小题正确的作出辅助线是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
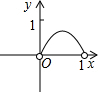
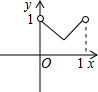
 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )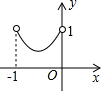
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=