题目内容
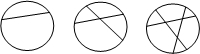
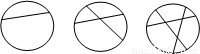
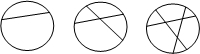 如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成
如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n | 0 | 1 | 2 | 3 | 4 | 5 | … | n |
| S | 1 | 2 | 4 | 7 |
分析:当切1刀时,S=1+1=2;当切2刀时,S=1+1+2=4;当切3刀时,S=1+1+2+3=7,…,则当切n刀时,S=1+1+2+3+4+…+n,然后把它们相加.
解答:解:n=1时,S=1+1=2,
n=2时,S=1+1+2=4,
n=3时,S=1+1+2+3=7,
n=4时,S=1+1+2+3+4=11,
…
所以当切n刀时,S=1+1+2+3+4+…+n=1+
n(n+1)=
n2+
n+1.
故答案为
n2+
n+1.
n=2时,S=1+1+2=4,
n=3时,S=1+1+2+3=7,
n=4时,S=1+1+2+3+4=11,
…
所以当切n刀时,S=1+1+2+3+4+…+n=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
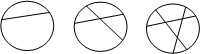 如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成________块(结果用n的代数式表示).
如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成________块(结果用n的代数式表示).