题目内容
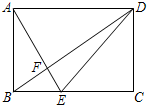 如图,在长方形ABCD(对边相等,四个角均为直角)中,点E在BC上,连接AE、BD、DE,AE交BD于F,则图中能确定面积相等但不全等的三角形共有
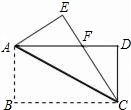
如图,在长方形ABCD(对边相等,四个角均为直角)中,点E在BC上,连接AE、BD、DE,AE交BD于F,则图中能确定面积相等但不全等的三角形共有
- A.4对
- B.3对
- C.2对
- D.0对
B
分析:根据要找出三角形面积相等但不全等的三角形,利用三角形面积公式等底等高面积相等,即可得出答案.
解答:∵S△ABD与S△ADE,底边为AD,高为AB,
∴S△ABD=S△ADE,
∴S△ABD-S△ADF=S△ADE-S△ADF,
∴S△ABF与S△DEF,
S△ABE与S△BDE,底边为BE,高为AB,
∴S△ABE=S△BDE,
∴图中能确定面积相等但不全等的三角形共有3对,
故选:B.
点评:此题主要考查了矩形的性质以及三角形面积公式应用,根据已知得出三角形的高与底边是解题关键.
分析:根据要找出三角形面积相等但不全等的三角形,利用三角形面积公式等底等高面积相等,即可得出答案.
解答:∵S△ABD与S△ADE,底边为AD,高为AB,
∴S△ABD=S△ADE,
∴S△ABD-S△ADF=S△ADE-S△ADF,
∴S△ABF与S△DEF,
S△ABE与S△BDE,底边为BE,高为AB,
∴S△ABE=S△BDE,
∴图中能确定面积相等但不全等的三角形共有3对,
故选:B.
点评:此题主要考查了矩形的性质以及三角形面积公式应用,根据已知得出三角形的高与底边是解题关键.

练习册系列答案
相关题目
 于点F.
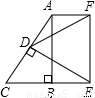
于点F.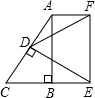 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.