��Ŀ����
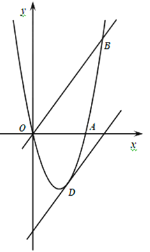
����Ŀ��ij�ֱ����ȼ���������߶�h���ף���ʱ��t���룩���Ϲ�ϵʽh��v0t+![]() gt2��0��t��2���������������ٶ�g��10��/��2���㣮���ֱ����ȼ����v0��20��/��ij��ٶ������������������У��������ٶ�gΪ��10��/��2���½������У��������ٶ�gΪ10��/��2��
gt2��0��t��2���������������ٶ�g��10��/��2���㣮���ֱ����ȼ����v0��20��/��ij��ٶ������������������У��������ٶ�gΪ��10��/��2���½������У��������ٶ�gΪ10��/��2��
��1�����ֱ����ڵ����ϵ�ȼ��������ʱ�����15�ף�
��2���ڱ����ȼ���1.5����1.8�����ʱ���ڣ��жϱ����������������½�����˵�����ɣ�
���𰸡���1��t��1����2�������������Σ����ɼ�����
��������
��1����֪g��v0��h��ֵ�����ʽ�ɽ��t��ֵ��
��2����������ɵ�h��20t��5t2����5��t2��4t+4��+20��Ȼ���֪�����������Σ�
�⣺��1�������⽫g����10��/��2��v0��20��/�룬h��15�״������ݣ��ã�
15��20t��5t2
��t2��4t+3��0��
������t��1����t��3����0
��t��1��t��3
�֡�0��t��2
��t��1��
��2��������������
h��20t��5t2����5��t2��4t+4��+20
����5��t��2��2+20
��t��2ʱ������ﵽ��ߵ㣮
����1.5s��1.8s�ڱ����������Σ�

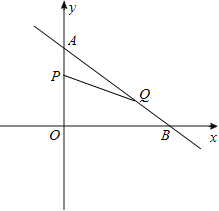
����Ŀ��2017����Ա�˫ʮһ������11������۶�ͻ��ʮ�ڣ�3�����ư��ڣ����ճɽ������1682��Ԫ�ϣ��ڽ����˫ʮһǰϦ��ij��ҵ����һ�ֱ�����Ʒ��Ϊ˫ʮһ��������Ʒ������֮ǰ�ij����г�������֣���Ʒ�����ܲ����ȶ���600������Ʒ����������a�������ɹ̶��������븡������������������ɣ����й̶����������ֲ��䣬�������������ۼ�x��Ԫ/������x��10���ɷ��ȣ��ҵõ������±����е���Ϣ��
�ۼ�x��Ԫ/���� | 5 | 8 |
��������Q������ | 580 | 400 |
��1����Q����x�ĺ�����ϵʽ��
��2����������������Ʒ���������꣬���ۼ�x��
��3�����ۼ�xΪ����ʱ�������۶������������ֵ��