Question

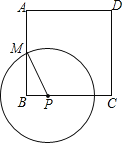
【题目】如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作．当与正方形ABCD的边相切时，BP的长为（ ）

A. 3B. C. 3或D. 不确定

Answer 1

【答案】C

【解析】

分两种情况讨论：点⊙P与直线CD相切时，PC=PM，设BP=x，利用勾股定理求出x值即可得答案；当⊙P与直线AD相切，设切点为K，连接PK，则PK⊥AD，PK=PM，可得四边形PCDK是矩形，则PM=PK=CD，根据勾股定理求出BP的长即可.

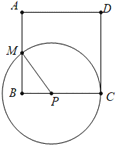
如图，点⊙P与直线CD相切时，设BP=x，则PM=PC=8-x，

∴PM2=BP2+，即(8-x)2=x2+42，

解得：x=3.

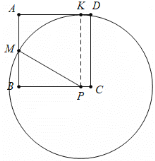
如图，当⊙P与直线AD相切时，设切点为K，连接PK，则PM=PK，

∵K为切点，

∴PK⊥AD，

∴四边形PCDK是矩形，

∴PK=CD，

∴PM=CD=8，

∴BP===.

综上所述：BP的长为3或.

故选C.