题目内容
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
![]()
(1)若线段AB=a,CE=b,|a﹣17|+(b﹣5.5)2=0,求线段AB、CE的长;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=20,AD=2BE,求线段CE的长.
【答案】(1)AB=17,CE=5.5;(2)7;(3)6.
【解析】
(1)由绝对值的非负性,平方的非负性,互为相反数的两个数和为0求出AB的长为17,CE的长为5.5;(2)线段的中点,线段的和差求出DE的长为7;(3)线段的中点,线段的和差求出CE的长为6.
解:(1)∵|a﹣17|+(b﹣5.5)2=0,
∴|a﹣17|=0,(b﹣5.5)2=0,
解得:a=17,b=5.5,
∵AB=a,CE=b,
∴AB=17,CE=5.5
(2)如图1所示:
![]()
∵点C为线段AB的中点,
∴AC=![]() =
=![]() =
=![]() ,
,
又∵AE=AC+CE,
∴AE=![]() +
+![]() =14,
=14,
∵点D为线段AE的中点,
∴DE=![]() AE=
AE=![]() =7;
=7;
(3)如图2所示:
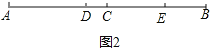
∵C为线段AB上的点,AB=20,
∴AC=BC=![]() =
=![]() =10,
=10,
又∵点D为线段AE的中点,AD=2BE,
∴AE=4BE,DE=![]() ,
,
又∵AB=AE+BE,
∴4BE+BE=20,
∴BE=4,AE=16,
又∵CE=BC﹣BE,
∴CE=10﹣4=6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目