题目内容
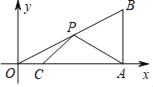
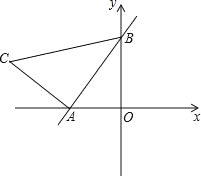
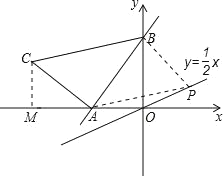
【题目】如图，直线y=kx+2与x轴、y轴分别交于A、B两点，OA：OB=
．以线段AB为边在第二象限内作等腰Rt△ABC，∠BAC=90°．
（1）求点A的坐标和k的值；
（2）求点C坐标；
（3）直线y=x在第一象限内的图象上是否存在点P，使得△ABP的面积与△ABC的面积相等？如果存在，求出点P坐标；如果不存在，请说明理由．
【答案】（1）A（﹣1，0），k=2；（2）C（﹣3，1）；（3）P坐标为（2，1）．
【解析】
（1）对于直线y=kx+2，令x=0求出y的值，确定出B坐标，得到OB的长，根据OA与OB比值求出OA的长，确定出A坐标，代入直线方程即可求出k的值；
（2）过C作CM垂直于x轴，利用同角的余角相等得到一对角相等，再由一对直角相等，以及AC=AB，利用AAS得到三角形ACM与三角形BAO全等，由全等三角形对应边相等得到CM=OA，AM=OB，由AM+OA求出OM的长，即可确定出C坐标；
（3）假设存在点P使得△ABP的面积与△ABC的面积相等，在直线y= 
x第一象限上取一点P，连接BP，AP，设点P（m，m），由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积，求出三角形AOB面积，两者相等求出m的值，即可确定出P坐标．
（1）对于直线y=kx+2，令x=0，得到y=2，即B（0，2），OB=2，
∵OA：OB=，∴OA=1，即A（﹣1，0），
将x=﹣1，y=0代入直线解析式得：0=﹣k+2，即k=2；
（2）过C作CM⊥x轴，可得∠AMC=∠BOA=90°，
∴∠ACM+∠CAM=90°，
∵△ABC为等腰直角三角形，即∠BAC=90°，AC=BA，
∴∠CAM+∠BAO=90°，
∴∠ACM=∠BAO，
在△CAM和△ABO中，
，
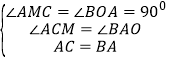∴△CAM≌△ABO（AAS），
∴AM=OB=2，CM=OA=1，即OM=OA+AM=1+2=3，
∴C（﹣3，1）；
（3）假设存在点P使得△ABP的面积与△ABC的面积相等，在直线y=x第一象限上取一点P，连接BP，AP，
设点P（m，m），
∴S△ABP=S△ABO+S△BPO﹣S△AOP=1+m﹣
m=1+
m，而S△ABC=ABAC=AB2=（12+22）=
，
可得1+m=，
解得：m=2，
则P坐标为（2，1）．
