题目内容
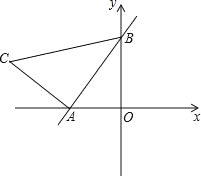
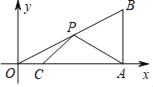
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
【答案】![]()
【解析】
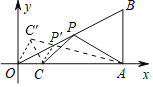
如图作点C关于直线OB的对称点C′,连接OC′,CC′,AC′,AC′交OB于P′,连接P′C,此时P′A+P′C的值最小,最小值为线段AC′的长.
如图作点C关于直线OB的对称点C′,连接OC′,CC′,AC′,AC′交OB于P′,连接P′C,此时P′A+P′C的值最小,最小值为线段AC′的长.
在Rt△OAB中,∵OA=3,AB=![]() ,
,
∴tan∠BOA=![]() ,
,
∴∠BOA=30°,
根据对称性可知:∠COC′=60°,OC=OC′=1,
∴△OCC′是等边三角形,
∴C′(![]() ,
,![]() ),
),
∵A(3,0),
∴AC′=![]() =
=![]() ,
,
∴PA+PC的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目