题目内容
已知抛物线 的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.

(1)求点A、B、C、D的坐标;
(2)在y轴的正半轴上是否存在点P,使以点P、O、A为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由;
(3)取点E( ,0)和点F(0,
,0)和点F(0, ),直线l经过E、F两点,点G是线段BD的中点.
),直线l经过E、F两点,点G是线段BD的中点.
①点G是否在直线l上,请说明理由;
②在抛物线上是否存在点M,使点M关于直线l的对称点在x轴上?若存在,求出点M的坐标;若不存在,请说明理由.
 的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
(1)求点A、B、C、D的坐标;
(2)在y轴的正半轴上是否存在点P,使以点P、O、A为顶点的三角形与△AOC相似?若存在,求出点P的坐标;若不存在,请说明理由;
(3)取点E(
 ,0)和点F(0,
,0)和点F(0, ),直线l经过E、F两点,点G是线段BD的中点.
),直线l经过E、F两点,点G是线段BD的中点.①点G是否在直线l上,请说明理由;
②在抛物线上是否存在点M,使点M关于直线l的对称点在x轴上?若存在,求出点M的坐标;若不存在,请说明理由.
解:(1)在 中,令y=0,则
中,令y=0,则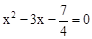 ,整理得,4x2﹣12x﹣7=0,
,整理得,4x2﹣12x﹣7=0,
解得x1=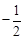 ,x2=
,x2=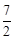 。∴A(
。∴A(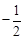 ,0),B(
,0),B(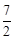 ,0)。
,0)。
在 中,令x=0,则y=
中,令x=0,则y= 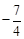 。∴C(0,
。∴C(0,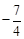 )。
)。
∵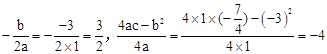 ,∴顶点D(
,∴顶点D(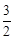 ,﹣4)。
,﹣4)。
(2)在y轴正半轴上存在符合条件的点P。
设点P的坐标为(0,y),
∵A(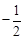 ,0),C(0,
,0),C(0,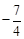 ),∴OA=
),∴OA= ,OC=
,OC=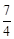 ,OP=y,
,OP=y,
①若OA和OA是对应边,则△AOP∽△AOC,∴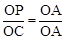 。∴y=OC=
。∴y=OC=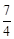 ,此时点P(0,
,此时点P(0,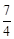 )。
)。
②若OA和OC是对应边,则△POA∽△AOC,∴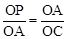 ,即
,即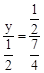 。
。
解得y=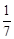 ,此时点P(0,
,此时点P(0,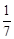 )。
)。
综上所述,符合条件的点P有两个,P(0,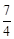 )或(0,
)或(0,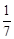 )。
)。
(3)①设直线l的解析式为y=kx+b(k≠0),
∵直线l经过点E( ,0)和点F(0,
,0)和点F(0, ),
),
∴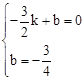 ,解得
,解得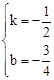 ,
,
∴直线l的解析式为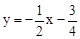 。
。
∵B(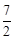 ,0),D(
,0),D(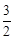 ,﹣4),
,﹣4),
∴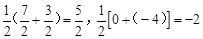 ,∴线段BD的中点G的坐标为(
,∴线段BD的中点G的坐标为( ,﹣2)。
,﹣2)。
当x= 时,
时,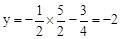 ,∴点G在直线l上。
,∴点G在直线l上。
②在抛物线上存在符合条件的点M。

设抛物线的对称轴与x轴交点为H,则点H的坐标为(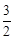 ,0),
,0),
∵E( ,0)、F(0,
,0)、F(0, ),B(
),B(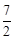 ,0)、D(
,0)、D(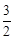 ,﹣4),
,﹣4),
∴OE=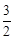 ,OF=
,OF=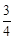 ,HD=4,HB=
,HD=4,HB=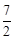 ﹣
﹣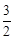 =2。
=2。
∵ ,∠OEF=∠HDB,
,∠OEF=∠HDB,
∴△OEF∽△HDB。∴∠OFE=∠HBD。
∵∠OEF+∠OFE=90°,∴∠OEF+∠HBD=90°。
∴∠EGB=180°﹣(∠OEF+∠HBD)
=180°﹣90°=90°,
∴直线l是线段BD的垂直平分线。
∴点D关于直线l的对称点就是点B。
∴点M就是直线DE与抛物线的交点。
设直线DE的解析式为y=mx+n,
∵D(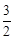 ,﹣4),E(
,﹣4),E( ,0),
,0),
∴ ,解得
,解得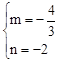 。
。
∴直线DE的解析式为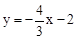 。
。
联立 ,解得
,解得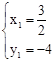 ,
,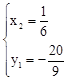 。
。
∴符合条件的点M有两个,是(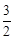 ,﹣4)或(
,﹣4)或(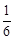 ,
,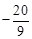 )。
)。
 中,令y=0,则
中,令y=0,则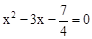 ,整理得,4x2﹣12x﹣7=0,
,整理得,4x2﹣12x﹣7=0,解得x1=
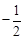 ,x2=
,x2=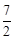 。∴A(
。∴A(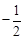 ,0),B(
,0),B(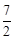 ,0)。
,0)。在
 中,令x=0,则y=
中,令x=0,则y= 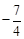 。∴C(0,
。∴C(0,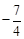 )。
)。∵
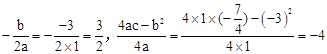 ,∴顶点D(
,∴顶点D(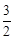 ,﹣4)。
,﹣4)。(2)在y轴正半轴上存在符合条件的点P。
设点P的坐标为(0,y),
∵A(
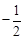 ,0),C(0,
,0),C(0,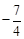 ),∴OA=
),∴OA= ,OC=
,OC=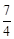 ,OP=y,
,OP=y,①若OA和OA是对应边,则△AOP∽△AOC,∴
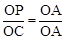 。∴y=OC=
。∴y=OC=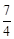 ,此时点P(0,
,此时点P(0,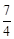 )。
)。②若OA和OC是对应边,则△POA∽△AOC,∴
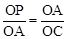 ,即
,即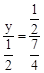 。
。解得y=
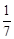 ,此时点P(0,
,此时点P(0,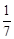 )。
)。综上所述,符合条件的点P有两个,P(0,
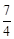 )或(0,
)或(0,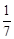 )。
)。(3)①设直线l的解析式为y=kx+b(k≠0),
∵直线l经过点E(
 ,0)和点F(0,
,0)和点F(0, ),
),∴
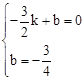 ,解得
,解得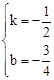 ,
,∴直线l的解析式为
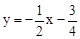 。
。∵B(
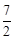 ,0),D(
,0),D(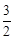 ,﹣4),
,﹣4),∴
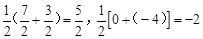 ,∴线段BD的中点G的坐标为(
,∴线段BD的中点G的坐标为( ,﹣2)。
,﹣2)。当x=
 时,
时,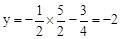 ,∴点G在直线l上。
,∴点G在直线l上。②在抛物线上存在符合条件的点M。

设抛物线的对称轴与x轴交点为H,则点H的坐标为(
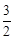 ,0),
,0),∵E(
 ,0)、F(0,
,0)、F(0, ),B(
),B(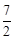 ,0)、D(
,0)、D(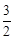 ,﹣4),
,﹣4),∴OE=
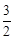 ,OF=
,OF=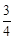 ,HD=4,HB=
,HD=4,HB=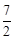 ﹣
﹣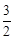 =2。
=2。∵
 ,∠OEF=∠HDB,
,∠OEF=∠HDB,∴△OEF∽△HDB。∴∠OFE=∠HBD。
∵∠OEF+∠OFE=90°,∴∠OEF+∠HBD=90°。
∴∠EGB=180°﹣(∠OEF+∠HBD)
=180°﹣90°=90°,
∴直线l是线段BD的垂直平分线。
∴点D关于直线l的对称点就是点B。
∴点M就是直线DE与抛物线的交点。
设直线DE的解析式为y=mx+n,
∵D(
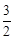 ,﹣4),E(
,﹣4),E( ,0),
,0),∴
 ,解得
,解得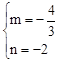 。
。∴直线DE的解析式为
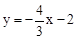 。
。联立
 ,解得
,解得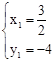 ,
,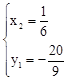 。
。∴符合条件的点M有两个,是(
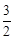 ,﹣4)或(
,﹣4)或(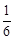 ,
,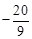 )。
)。试题分析:(1)令y=0,解关于x的一元二次方程求出A、B的坐标,令x=0求出点C的坐标,再根据顶点坐标公式计算即可求出顶点D的坐标。
(2)根据点A、C的坐标求出OA、OC的长,再分OA和OA是对应边,OA和OC是对应边两种情况,利用相似三角形对应边成比例列式求出OP的长,从而得解。
(3)①设直线l的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式求出直线l的解析式,再利用中点公式求出点G的坐标,然后根据直线上点的坐标特征验证即可。
②设抛物线的对称轴与x轴交点为H,求出OE、OF、HD、HB的长,然后求出△OEF和△HDB相似,根据相似三角形对应角相等求出∠OFE=∠HBD,然后求出EG⊥BD,从而得到直线l是线段BD的垂直平分线,根据线段垂直平分线的性质点D关于直线l的对称点就是B,从而判断出点M就是直线DE与抛物线的交点。再设直线DE的解析式为y=mx+n,利用待定系数法求一次函数解析求出直线DE的解析式,然后与抛物线解析式联立求解即可得到符合条件的点M。

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
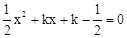 .
.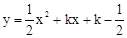 的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
 图象上部分点的坐标满足下表:
图象上部分点的坐标满足下表: ,当自变量x取m对应的函数值大于0,设自变量分别取m-3,m+3 时对应的函数值为y1,y2,则
,当自变量x取m对应的函数值大于0,设自变量分别取m-3,m+3 时对应的函数值为y1,y2,则