题目内容
已知:一元二次方程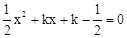 .
.
(1)求证:不论k为何实数时,此方程总有两个实数根;
(2)设k<0,当二次函数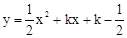 的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
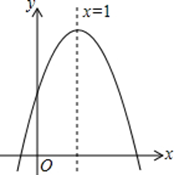
(3)在(2)的条件下,若抛物线的顶点为C,过y轴上一点M(0,m)作y轴的垂线l,当m为何值时,直线l与△ABC的外接圆有公共点?
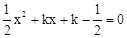 .
.(1)求证:不论k为何实数时,此方程总有两个实数根;
(2)设k<0,当二次函数
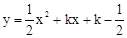 的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;(3)在(2)的条件下,若抛物线的顶点为C,过y轴上一点M(0,m)作y轴的垂线l,当m为何值时,直线l与△ABC的外接圆有公共点?
解:(1)证明:∵ ,
,
∴关于x的一元二次方程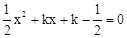 ,不论k为何实数时,此方程总有两个实数根。
,不论k为何实数时,此方程总有两个实数根。

(2)令y=0,则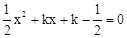 。
。
∵ ,
,
∴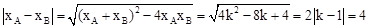 ,即
,即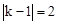 ,
,
解得k=3或k=﹣1。
∵k<0,∴k=﹣1。
∴此二次函数的解析式是 。
。
(3)由(2)知,抛物线的解析式是 ,
,
易求A(﹣1,0),B(3,0),C(1,﹣2),
∴AB=4,AC=2 ,BC=2
,BC=2 。
。
∴AC2+BC2=AB2。
∴△ABC是等腰直角三角形.AB为斜边。
∴外接圆的直径为AB=4。∴﹣2≤m≤2。
 ,
,∴关于x的一元二次方程
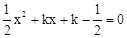 ,不论k为何实数时,此方程总有两个实数根。
,不论k为何实数时,此方程总有两个实数根。
(2)令y=0,则
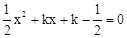 。
。∵
 ,
,∴
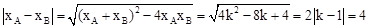 ,即
,即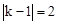 ,
,解得k=3或k=﹣1。
∵k<0,∴k=﹣1。
∴此二次函数的解析式是
 。
。(3)由(2)知,抛物线的解析式是
 ,
,易求A(﹣1,0),B(3,0),C(1,﹣2),
∴AB=4,AC=2
 ,BC=2
,BC=2 。
。∴AC2+BC2=AB2。
∴△ABC是等腰直角三角形.AB为斜边。
∴外接圆的直径为AB=4。∴﹣2≤m≤2。
(1)根据一元二次方程的根的判别式△=b2﹣4ac的符号来判定已知方程的根的情况。
(2)利用根与系数的关系 列出关于k的方程,通过解方程来求k的值。
列出关于k的方程,通过解方程来求k的值。
(3)根据直线与圆的位置的位置关系确定m的取值范围。
(2)利用根与系数的关系
 列出关于k的方程,通过解方程来求k的值。
列出关于k的方程,通过解方程来求k的值。(3)根据直线与圆的位置的位置关系确定m的取值范围。

练习册系列答案
相关题目
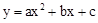 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).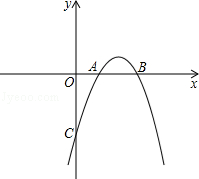
 的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
 ,0)和点F(0,
,0)和点F(0, ),直线l经过E、F两点,点G是线段BD的中点.
),直线l经过E、F两点,点G是线段BD的中点.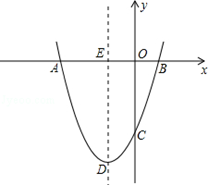
 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
 的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④b+2a=0;⑤a+b+c<0.其中正确的个数是【 】
的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④b+2a=0;⑤a+b+c<0.其中正确的个数是【 】