题目内容
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
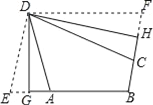
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°﹣3∠A.
∵0<∠ADC<180°,
∴0°<360°﹣3∠A<180°,
∴60°<∠A<120°;
(2)证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

