题目内容
【题目】已知某服装厂现有甲种布料50米,乙种布料27米,现计划用这两种布料生产A,B两种型号的时装共60套. 已知做一套A型号的时装需用甲种布料1米,乙种布料0.2米,可获利30元;做一套B型号的时装需用甲种布料0.5米,乙种布料0.8米,可获利20元. 设生产A型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式,并求出自变量的取值范围.
(2)当生产A型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
【答案】(1)![]() ;(2)当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
;(2)当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
【解析】1)关系式为:B种型号的时装件数×1+A种型号的时装件数×0.5≤50;B种型号的时装件数×0.2+A种型号的时装件数×0.8≤27;
(2)根据(1)中的结果得到结论.
解:(1)![]()
根据题意,得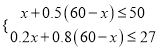
解得 ![]()
∵x是整数
∴x=35,36,37,38,39,40
∴y与x之间的函数表达式为![]()
(2)∵k=10>0
∴y随x的增大而增大
∴当x=40时,y有最大值为10×40+1200=160
答:当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
“点睛”此题是一道方案设计题,有一定的开放性.解决本题的关键是读懂题意,找到符合题意的不等关系:加工服装所用布料不大于布料总数,列不等式解答即可.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目