题目内容
【题目】如图,![]() 为
为![]() 的外接圆,
的外接圆,![]() ,作直线
,作直线![]() ,
,![]() 于
于![]() .
.
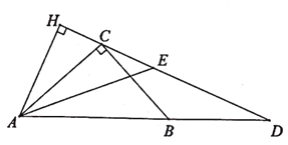
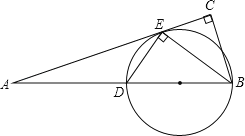
(1)图1,求证:![]() 是
是![]() 的切线;
的切线;
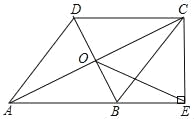
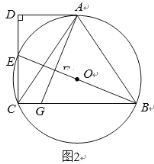
(2)图2,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)证明见详解;(2)①证明见详解;②![]() .
.
【解析】
(1)连接OA,OB,OC,由AC=AB,OA=OA,OC=OB可证出△OAC≌△OAB(SSS),利用全等三角形的性质可得出∠OAC=∠OAB,即AO平分∠BAC,利用垂径定理可得出AO⊥BC,结合AD//BC可得出AD⊥AO,由此即可证出AD是⊙O的切线;
(2)①连接AE,由圆内接四边形对角互补结合∠BCE=90°可得出∠BAE=90°,由同角的余角相等可得出∠BAG=∠AEB,结合∠ABC=∠ACB=∠AEB可得出∠BAG=∠ABC,由平行线的性质可得∠BAD+∠ABC=180°,即可得结论;
②由∠ADC=∠AFB=90°,∠ACD=∠ABF,AC=AB可证出△ADC≌△AFB(AAS),利用全等三角形的性质可求出AF,BF的长,设FG=x,在Rt△BFG中,利用勾股定理可求出x的值,即可求解.
证明:(1)如图1,连接OA,OB,OC.
在△OAC和△OAB中, ,
,
∴△OAC≌△OAB(SSS),
∴∠OAC=∠OAB,
∴AO平分∠BAC,
∴AO⊥BC.
又∵AD//BC,
∴AD⊥AO,
∴AD是⊙O的切线.
(2)①证明:如图2,连接AE.
∵AD//BC,AD⊥CD,
∴∠BCE=90°,
∴∠BAE=90°.
又∵AF⊥BE,
∴∠AFB=90°.
∵∠BAG+∠EAF=∠AEB+∠EAF=90°,
∴∠BAG=∠AEB.
∵∠ABC=∠ACB=∠AEB,
∴∠BAG=∠ABC,
∵AD//BC,
∴∠BAD+∠ABC=180°,
∴∠BAD+∠BAG=180°;
②在△ADC和△AFB中, ,
,
∴△ADC≌△AFB(AAS),
∴AF=AD=3,BF=CD=4,
∵∠BAG=∠ABC,
∴AG=BG
设FG=x,在Rt△BFG中,FG=x,BF=4,BG=AG=x+3,
∴FG2+BF2=BG2,即x2+42=(x+3)2,
∴x=![]() ,
,
∴FG=![]() .
.