题目内容
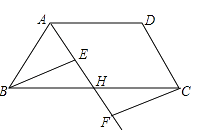
【题目】(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
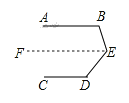
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
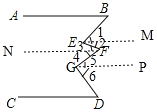
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?

【答案】(1)理由见解析
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
【解析】试题分析:已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
试题解析:(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,∴CD∥EF.∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)若∠B+∠D=∠E,由EF∥AB,得∠B=∠BEF,
∵∠E=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF,∴EF∥CD,
∴AB∥CD;
(3) 若将点E移至图2所示位置,过E作EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∠B+∠D+∠E=360°.
(4)∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B;

(5) 如图,作EM∥AB,FN∥AB,GP∥AB
∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D
∴∠1+∠2=∠E,5+∠6=∠G,∠3+∠4=∠F
∴E+∠G=∠B+∠F+∠D.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.