题目内容
【题目】如图,已知在矩形![]() 中,,
中,,![]() 以边
以边![]() 所在的直线为轴建立平面直角坐标系
所在的直线为轴建立平面直角坐标系![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点,将点
轴正半轴上的动点,将点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,使点
,使点![]() 恰好落在反比例
恰好落在反比例![]() 的图象上,则
的图象上,则![]() 的值是__________.
的值是__________.
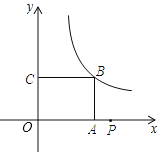
【答案】4
【解析】
利用矩形的性质先写出B点的坐标,再求出反比例函数的解析式,根据旋转的性质易证△BAP≌△PDB′,从而得到B′点的坐标,代入反比例函数的解析式即可解决问题.
解:∵在矩形OABC中,OA=3,OC=2,
∴AB=OC=2,点B的坐标为(3,2),
∴反比例函数的解析式为y=![]() (x>0).
(x>0).
设点B绕点P顺时针旋转90°后到点B′的位置,过点B′作B′D⊥x轴于D,则△BAP≌△PDB′,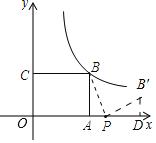
∴BA=PD=2,PA=B′D=t-3,
∴点B′的坐标为(t+2,t-3),
又∵点B′恰好落在反比例y=![]() (x>0)的图象上,
(x>0)的图象上,
∴(t+2)(t-3)=6,解得:t1=4,t2=-3(舍去),
∴t=4.
故答案为:4.

 阅读快车系列答案
阅读快车系列答案【题目】入学考试前,某语文老师为了了解所任教的甲、乙两班学生假期向的语文基础知识背诵情况,对两个班的学生进行了语文基础知识背诵检测,满分100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理,描述和分析(成绩得分用x表示,共分为五组:
A.0≤x<80,B.80≤x<85,C.85≤x<90,D.90≤x<95,E.95≤x<100),下面给出了部分信息:
甲班20名学生的成绩为:
甲组 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名学生的成绩在D组中的数据是:93,91,92,94,92,92,92
甲、乙两班抽取的学生成绩数据统计表
班级 | 甲组 | 乙组 |
平均数 | 91 | 92 |
中位数 | 91 | b |
众数 | c | 92 |
方差 | 41.2 | 27.3 |
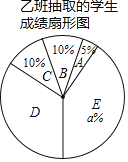
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值:a= ;b= ;c= ;
(2)根据以上数据,你认为甲、乙两个班中哪个班的学生基础知识背诵情况较好?请说明理由(一条理由即可);
(3)若甲、乙两班总人数为125,且都参加了此次基础知识检测,估计此次检测成绩优秀(x≥95)的学生人数是多少?