题目内容
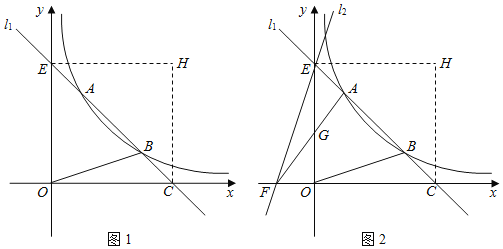
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
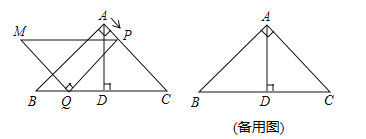
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)待定系数法求一次函数解析式和反比例函数解析式,将已知点坐标代入并解方程(组)即可;
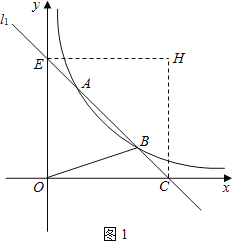
(2)先求出直线l1与坐标轴的交点坐标,可得:△COE是等腰直角三角形,再由翻折可得:OCHE是正方形.即可求出H的坐标;
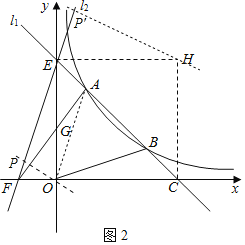
(3)①先待定系数法求直线AO解析式为y=3x,再由△AEG的面积与△OFG的面积相等可得:EF∥AO,即可求直线l2的解析式;
②存在,由S△PBC=S△OBC可知:点P在经过点O或H平行于直线l1:y=-x+4的直线上,易求得点P的坐标为P(-1,1)或P(1,7).
解:(1)将![]() 、点
、点![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() 双曲线的解析式为:
双曲线的解析式为:![]() .
.
(2)如图1中,
在![]() 中,令
中,令![]() ,得:
,得:![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,
由翻折得:![]()
![]() ,
,![]()
![]() 是正方形.
是正方形.
![]() .
.
(3)如图2,连接![]() ,
,
①![]() 、
、![]() .设直线
.设直线![]() 解析式为
解析式为![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
![]()
![]()
![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
②存在,点![]() 坐标为:
坐标为:![]() 或
或![]() .
.
解方程组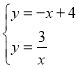 得:
得:![]() ,
,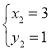 ;
;
![]() ;
;
![]() ,
,
![]() 点
点![]() 在经过点
在经过点![]() 或
或![]() 平行于直线
平行于直线![]() 的直线上,
的直线上,
易得:![]() 或
或![]()
分别解方程组![]() 或
或![]() 得:
得:![]() 或
或![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目