题目内容
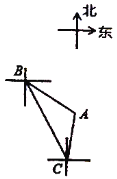
【题目】如图,轮船从![]() 处以每小时60海里的速度沿南偏东
处以每小时60海里的速度沿南偏东![]() 方向匀速航行,在
方向匀速航行,在![]() 处观测灯塔
处观测灯塔![]() 位于南偏东
位于南偏东![]() 方向上,轮船航行40分钟到达
方向上,轮船航行40分钟到达![]() 处,在
处,在![]() 处观测灯塔
处观测灯塔![]() 位于北偏东
位于北偏东![]() 方向上,求
方向上,求![]() 处与灯塔
处与灯塔![]() 的距离.
的距离.
【答案】![]() 处与灯塔
处与灯塔![]() 的距离是
的距离是![]() 海里.
海里.
【解析】
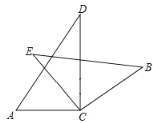
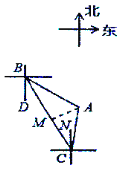
作AM⊥BC于M.由题意得,∠DBC=20°,∠DBA=50°,![]() 海里,∠NCA=10°,则∠ABC=∠ABD-∠CBD=30°.由BD∥CN,得出∠BCN=∠DBC=20°,那么∠ACB=∠ACN+∠BCN=30°=∠ABC,根据等角对等边得出AB=AC,由等腰三角形三线合一的性质得到
海里,∠NCA=10°,则∠ABC=∠ABD-∠CBD=30°.由BD∥CN,得出∠BCN=∠DBC=20°,那么∠ACB=∠ACN+∠BCN=30°=∠ABC,根据等角对等边得出AB=AC,由等腰三角形三线合一的性质得到![]() 海里.然后在直角△ACM中,利用余弦函数的定义得出
海里.然后在直角△ACM中,利用余弦函数的定义得出![]() ,代入数据计算即可.
,代入数据计算即可.
解:如图,作![]() 于
于![]() .
.
由题意得,![]() ,
,![]() ,
,![]() (海里),
(海里),![]() ,
,
则![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 于
于![]() ,
,
∴![]() (海里)
(海里)
在直角![]() 中,
中,![]() ;
;![]() ,
,
∴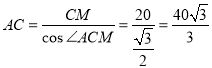 (海里).
(海里).
答:![]() 处与灯塔
处与灯塔![]() 的距离是
的距离是![]() 海里.
海里.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的对应值如图,下列说法错误的是:( )
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是(0,4)
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而增大