题目内容
本题为选项做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
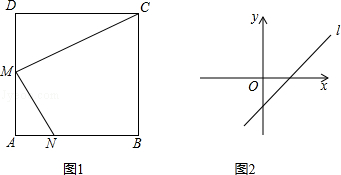
甲:直线l:y=(m﹣3)x+n﹣2(m,n为常数)的图象如图1所示,化简:|m﹣n|﹣ ;
;
乙:已知:如图2,在边长为a的正方形ABCD中,M是边AD的中点,能否在边AB上找到点N(不含A、B),使得△MAN相似?若能,请给出证明;若不能,请说明理由.

甲:直线l:y=(m﹣3)x+n﹣2(m,n为常数)的图象如图1所示,化简:|m﹣n|﹣
 ;
;乙:已知:如图2,在边长为a的正方形ABCD中,M是边AD的中点,能否在边AB上找到点N(不含A、B),使得△MAN相似?若能,请给出证明;若不能,请说明理由.
试题分析:(1)根据函数图象确定m、n的取值范围,再化简.
(2)作NM⊥CM即可,可根据相似三角形的判定来证明.
解(甲题)由图象可知:m﹣3>0且n﹣2<0,(2分)
∴m>3且n<2.(4分)
|m﹣n|﹣
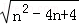 ﹣|m﹣1|=m﹣n﹣(2﹣n)﹣(m﹣1)(7分)
﹣|m﹣1|=m﹣n﹣(2﹣n)﹣(m﹣1)(7分)=﹣1(9分)
(乙题)猜想:当AN=
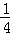 a时,△CDM∽△MAN.(2分)
a时,△CDM∽△MAN.(2分)证明:在△CDM和△MAN中,
∵∠CDM=∠MAN=90°,
M是AD的中点,且四边形ABCD为正方形,(3分)
∴AM=DM=
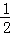 a,(4分)
a,(4分)∴
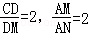 ,(6分)
,(6分)∴
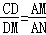 (7分)
(7分)∴△CDM∽△MAN.(9分)
点评:甲题根据一次函数与系数的关系确定m、n的取值范围,然后化简.乙题考查相似三角形的判定.

练习册系列答案
相关题目
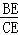 = .
= . = ;
= ;
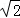
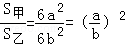 ,又设V甲、V乙分别表示这两个正方体的体积,则
,又设V甲、V乙分别表示这两个正方体的体积,则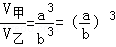 .
.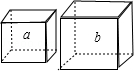
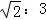 ,那么它们的面积之比为 .
,那么它们的面积之比为 .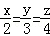 ,2x﹣3y+4z=22,求:代数式x+y﹣z的值.
,2x﹣3y+4z=22,求:代数式x+y﹣z的值.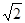 ,点A的坐标为(2,0),则E点的坐标为__________________。
,点A的坐标为(2,0),则E点的坐标为__________________。