题目内容
【题目】如图,抛物线y=a(x+3)(x﹣k)交x轴于点A、B,(A左B右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(﹣3,0);②a=﹣
,则下列结论:①A点坐标(﹣3,0);②a=﹣![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
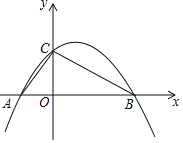
A.4B.3C.2D.1
【答案】A
【解析】
令y=0,求得A点坐标,B点用字母k表示的坐标,再把抛物线的解析式化成一般形式,则可用a与k的代数式表示OC,进而根据sin∠CBA=![]() ,用a与k的代数式表示BC,在由勾股定理得出a与k的方程,求得a的值,再根据△AOC的周长为12,求得k的值,则题目中的问题便可解决.
,用a与k的代数式表示BC,在由勾股定理得出a与k的方程,求得a的值,再根据△AOC的周长为12,求得k的值,则题目中的问题便可解决.
令y=0,则y=a(x+3)(x﹣k)=0,
解得x=﹣3或k,
∴A(﹣3,0),B(k,0),
故①正确;
∵y=a(x+3)(x﹣k)=ax2+(3a﹣ak)x﹣3ak,
∴C(0,﹣3ak),
∴OC=﹣3ak,
∵sin∠CBA=![]() ,
,
∴![]() ,
,
∴BC=![]() ,
,
∵BC2﹣OC2=OB2,
∴45a2k2﹣9a2k2=k2,
∴a2=![]() ,
,
∵抛物线的开口向下,
∴a=﹣![]() ,
,
故②正确;
∴OC=![]() k,
k,
∴AC=![]() ,
,
∵△AOC的周长为12,
∴3+![]() k+
k+![]() =12,
=12,
解得,k=8,
∴B(8,0),
故③正确;
∵A(﹣3,0),B(8,0),
∴对称轴为:x=![]() ,
,
故④正确.
综上所述①②③④都正确
故选:A.

练习册系列答案
相关题目