题目内容
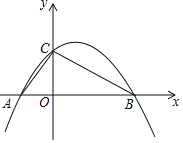
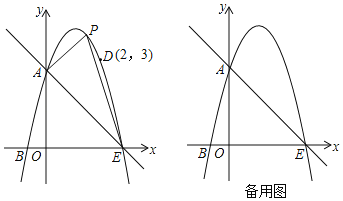
【题目】如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E,点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;(2)t=![]() 时,△PAE的面积最大,最大值是
时,△PAE的面积最大,最大值是![]() ;(3)t的值为1或
;(3)t的值为1或![]() .
.
【解析】
(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)由抛物线的对称性可求得E点坐标,从而可求得直线EA的解析式,作PM∥y轴,交直线AE于点M,则可用t表示出PM的长,从而可表示出△PAE的面积,再利用二次函数的性质可求得其最大值即可;
(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.
解:(1)由题意得: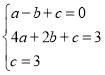 ,
,
解得: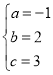 ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(0,3),D(2,3),
∴抛物线对称轴为x=1,
∴E(3,0),
设直线AE的解析式为y=kx+3,
∴3k+3=0,解得,k=﹣1,
∴直线AE的解析式为y=﹣x+3,
如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),
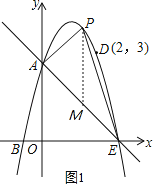
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,
∴![]() =
=![]() =
=![]() ,
,
∴t=![]() 时,△PAE的面积最大,最大值是
时,△PAE的面积最大,最大值是![]() .
.
(3)由图可知∠PEA≠90°,
∴只能有∠PAE=90°或∠APE=90°,
①当∠PAE=90°时,如图2,作PG⊥y轴,

∵OA=OE,
∴∠OAE=∠OEA=45°,
∴∠PAG=∠APG=45°,
∴PG=AG,
∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),
②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,
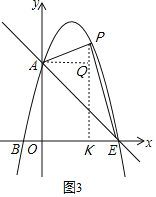
则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,
∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,
∴∠PAQ=∠KPE,且∠PKE=∠PQA,
∴△PKE∽△AQP,
∴![]() ,
,
∴![]() ,
,
即t2﹣t﹣1=0,解得:t=![]() 或t=
或t=![]() <0(舍去),
<0(舍去),
综上可知存在满足条件的点P,t的值为1或![]() .
.

【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |
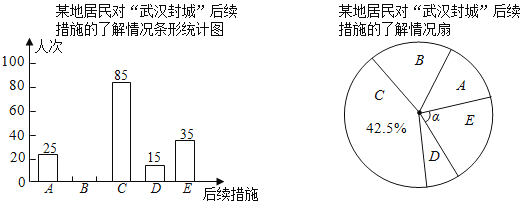
已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.