题目内容
函数y=ax2(a≠0)的图象与直线y=2x-3交于点(1,b).
(1)求a和b的值.
(2)求抛物线y=ax2的解析式,并求出顶点坐标和对称轴.
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大?
(4)求抛物线与直线y=-2的两个交点及顶点所构成的三角形的面积.
(1)求a和b的值.
(2)求抛物线y=ax2的解析式,并求出顶点坐标和对称轴.
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大?
(4)求抛物线与直线y=-2的两个交点及顶点所构成的三角形的面积.
(1)把点(1,b)代入y=2x-3得2-3=b,解得b-=1,
所以交点坐标为(1,-1),
把(1,-1)代入y=ax2得-1=a,即a=-1;
(2)当a=-1时,二次函数解析式为y=-x2,
所以抛物线的对称轴为y轴,顶点坐标为(0,0);
(3)二次函数y=-x2,当x<0时,y随x的增大而增大;
(4)如图,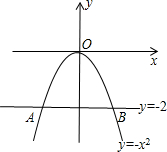 解方程组
解方程组
或
,
所以A点坐标为(-
,-2),B点坐标为(
,-2),
所以S△OAB=
×2×2
=2
.
所以交点坐标为(1,-1),
把(1,-1)代入y=ax2得-1=a,即a=-1;
(2)当a=-1时,二次函数解析式为y=-x2,
所以抛物线的对称轴为y轴,顶点坐标为(0,0);
(3)二次函数y=-x2,当x<0时,y随x的增大而增大;
(4)如图,
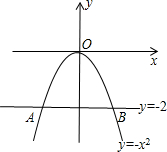 解方程组
解方程组
|
|
|
所以A点坐标为(-
| 2 |
| 2 |
所以S△OAB=
| 1 |
| 2 |
| 2 |
| 2 |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
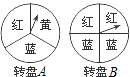 个转盘.
个转盘.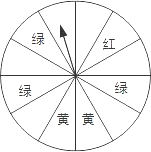 元的购书券,凭购书券可以在书城继续购书,如果读者不愿意转转盘,那么可以直接获得10元的购书券.
元的购书券,凭购书券可以在书城继续购书,如果读者不愿意转转盘,那么可以直接获得10元的购书券.
