题目内容
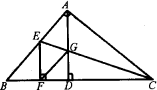
在△ABC中，∠BAC＝90°，AD⊥BC，垂足为点D，CE平分∠ACB，交AD于点G，交AB于点E，EF⊥BC，垂足为F，求证：四边形AEFG是菱形．
答案：
解析：
解析：
|
证明：∵CE平分∠ACB，EF⊥BC，∠BAC＝90°， ∴AE＝EF，∠AEC＝∠FEC． ∵EF⊥BC，AD⊥BC， ∴EF∥AD． ∴∠AGE＝∠FEG＝∠AEC． ∴AE＝AG． 同理EF＝FC． ∴AE＝EF＝FG＝AG ∴四边形AEFG是菱形． |
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以4cm/s的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．
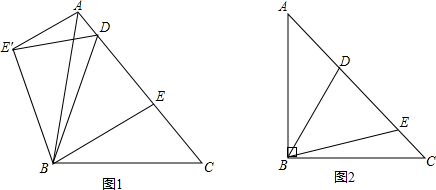
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以每秒4cm，的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．