题目内容
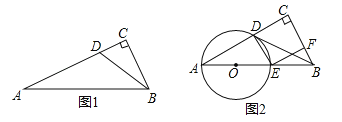
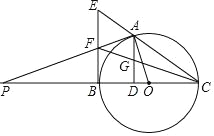
【题目】如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.
(1)求证:BF=EF;
(2)求tanP;
(3)求⊙O的半径r.
【答案】(1)证明见解析;(2)tanP=![]() ;(3)r=3
;(3)r=3![]() .
.
【解析】
(1)根据已知条件得到∠EBC=∠ADC=90°,根据平行线分线段成比例定理的![]() ,等量代换即可得到结论;
,等量代换即可得到结论;
(2)连接AB,根据圆周角定理得到∠BAC=∠BAE=90°,推出FA=FB=FE=FG=3,过点F作FH⊥AG交AG于点H,推出四边形FBDH是矩形,得到FB=DH=3,根据勾股定理得到FH=![]() ,根据平行线的性质得到∠AFH=∠APD,根据锐角三角函数的定义即可得到结论;
,根据平行线的性质得到∠AFH=∠APD,根据锐角三角函数的定义即可得到结论;
(3)设半径为r,根据勾股定理列方程即可得到结论.
(1)∵EB是切线,AD⊥BC,
∴∠EBC=∠ADC=90°,
∴AD∥EB,
∴![]() ,
,
∵AG=GD,
∴EF=FB;
(2)连接AB,
∵BC是直径,
∴∠BAC=∠BAE=90°,
∵EF=FB,
∴FA=FB=FE=FG=3,
过点F作FH⊥AG交AG于点H,
∵FA=FG,FH⊥AG,
∴AH=HG,
∵∠FBD=∠BDH=∠FHD=90°,
∴四边形FBDH是矩形,
∴FB=DH=3,
∵AG=GD,
∴AH=HG=1,GD=2,FH=![]()
∵FH∥PD,
∴∠AFH=∠APD,
∴tanP=tan∠AFH=![]() ;
;
(3)设半径为r,在RT△ADO中,
∵AO2=AD2+OD2,
∴r2=42+(r﹣2![]() )2,
)2,
.∴r=3![]() .
.


练习册系列答案
相关题目