题目内容
【题目】如图![]() 的网格中,每个小正方形的边长均为
的网格中,每个小正方形的边长均为![]() ,线段
,线段![]() 的端点都在小正方形的顶点上.(要求:下面所画图形的点
的端点都在小正方形的顶点上.(要求:下面所画图形的点![]() 都在小正方形的顶点上)
都在小正方形的顶点上)
![]() 在图
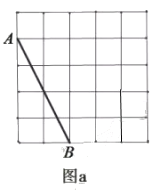
在图![]() 中画一个以线段
中画一个以线段![]() 为一边的等腰三角形
为一边的等腰三角形![]() ,
,![]() ,使
,使![]() 的面积是
的面积是![]() .
.
![]() 在图
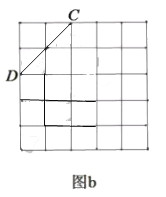
在图![]() 中画一个以线段
中画一个以线段![]() 为一边的矩形
为一边的矩形![]() ,使矩形
,使矩形![]() 的面积是
的面积是![]() ,并直接写出矩形
,并直接写出矩形![]() 的周长
的周长
【答案】![]() 画图见解析;
画图见解析;![]() 画图见解析,矩形
画图见解析,矩形![]() 的周长是
的周长是![]()
【解析】
(1)先画出图形,然后根据勾股定理和等腰三角形的性质来验证即可;
(2)先画出图形,然后根据勾股定理和矩形的性质来验证即可,然后再根据矩形的周长公式求出即可.
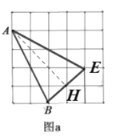
解:(1)如图所示:
由题意可知AB=AE=![]() ,
,
BE=![]() ,
,
作AH⊥BE,由等腰三角形的性质可得BH=![]() ,
,
在RT△ABH中,AH=![]() ,
,
∴S△ABE=![]() =
=![]() =6.
=6.
故所画图形符合题意;
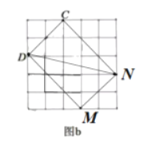
(2)如图所示:
由题意可知CD=MN=![]() ,
,
DM=CN=![]() ,
,
连接DN,则DN=![]() ,
,
∴ DM2+MN2=18+8=26=DN2,
∴∠M=90°,同理可证∠ C=∠CDM=∠CNM=90°,
∴四边形CDMN是矩形,面积=CD×DM=![]() =12,故所画图形符合题意,
=12,故所画图形符合题意,
矩形周长=2(CD+DM)=2×(![]() )=
)=![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
获得好评的电影部数 | 56 | 10 | 45 | 50 | 160 | 51 |
(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率:
(2)电影公司为增加投资回报,需在调查前根据经验预估每类电影的好评率(好评率是指:一类电影中获得好评的部数与该类电影的部数的比值),如表所示:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
预估好评率 | 0.5 | 0.2 | 0.15 | 0.15 | 0.4 | 0.3 |
定义统计最![]() 其中
其中![]() 为第i类电影的实际好评率,
为第i类电影的实际好评率,![]() 为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。
为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。