题目内容
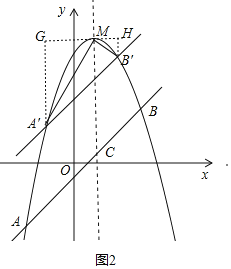
【题目】已知，如图，抛物线y＝ax2+bx+c（a≠0）的顶点为M（1，9），经过抛物线上的两点A（﹣3，﹣7）和B（3，m）的直线交抛物线的对称轴于点C．
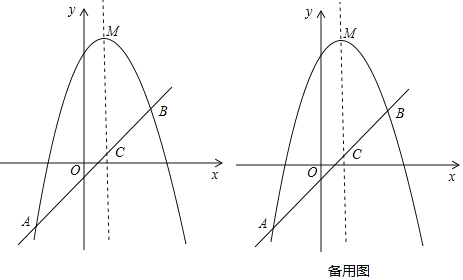
（1）求抛物线的解析式及点B的坐标．
（2）在抛物线上A，M两点之间的部分（不包含A，M两点），是否存在点D，使得S△DAC＝2S△DCM？若存在，求出点D的坐标；若不存在，请说明理由．
（3）上下平移直线AB，设平移后的直线与抛物线交与A′，B′两点（A′在左边，B'在右边），且与y轴交与点P（0，n），若∠A′MB′＝90°，求n的值．
【答案】（1）y＝﹣x2+2x+8，B（3，5）；（2）存在，点D（﹣1，5）；（3）n＝3
【解析】
（1）抛物线的表达式为：y＝a（x﹣1）2+9，将点A的坐标代入上式并解得：a＝﹣1，即可求解；
（2）S△DAC＝2S△DCM，则HN＝2GH，即1﹣k﹣（3k﹣7）＝2（9﹣k﹣1+k），即可求解；
（3）∠GA′M＝∠HMB′，故tan∠GA′M＝tan∠HMB′，即：
，而x1+x2＝0，x1x2＝n﹣8，y1+y2＝2n，y1y2＝4n﹣32+n2，即可求解．
解：（1）抛物线的表达式为：y＝a（x﹣1）2+9，
将点A的坐标代入上式并解得：a＝﹣1，
故抛物线的表达式为：y＝﹣x2+2x+8，
将点B坐标代入上式并解得：m＝5，
故点B（3，5）；
（2）过点M、C、A分别作三条相互平移的平行线，分别交y轴于点G、H、N，直线l与抛物线交于点D，
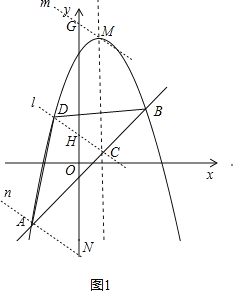
设直线m的表达式为：y＝kx+t，将点M的坐标代入上式并解得：t＝9﹣k，
故直线m的表达式为：y＝kx+9﹣t，即点G（0，9﹣t），
同理直线l的表达式为：y＝kx+1﹣k，故点H（0，1﹣k），
同理直线n的表达式为：y＝kx+3k﹣7，故点N（0，3k﹣7），
S△DAC＝2S△DCM，则HN＝2GH，
即1﹣k﹣（3k﹣7）＝2（9﹣k﹣1+k），
解得：k＝﹣2，
故直线l的表达式为：y＝﹣2x+3…②，
联立①②并解得：x＝5（舍去）或﹣1，
故点D（﹣1，5）；
（3）直线A′B′的表达式为：y＝2x+n，
设点A′、B′的坐标分别为：（x1，y1）、（x2，y2），
将抛物线与直线A′B′的表达式联立并整理得：
x2+n﹣8＝0，
故x1+x2＝0，x1x2＝n﹣8，
y1+y2＝2（x1+x2）+2n＝2n，同理可得：y1y2＝4n﹣32+n2，
过点M作x轴的平行线交过点A′与y轴的平行线于点G，交过点B′与y轴的平行线于点H，
∵∠A′MB′＝90°，
∴∠GMA′+∠GA′M＝90°，∠GMA′+∠MHB′＝90°，
∴∠GA′M＝∠HMB′，故tan∠GA′M＝tan∠HMB′，
即：，
而x1+x2＝0，x1x2＝n﹣8，y1+y2＝2n，y1y2＝4n﹣32+n2，
整理得：n2﹣13n+30＝0，
解得：n＝3或10（舍去10），
故n＝3．
