题目内容
【题目】某种商品每天的销售利润![]() 元,销售单价
元,销售单价![]() 元,间满足函数关系式:
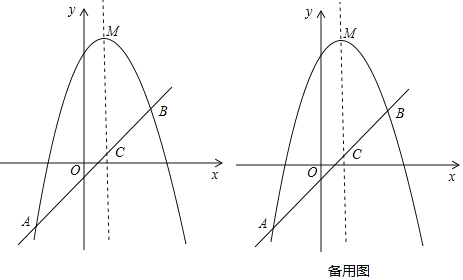
元,间满足函数关系式:![]() ,其图象如图所示.
,其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大? 最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于21 元?

【答案】(1)10,25;(2)![]() .
.
【解析】
(1)将点![]() 代入
代入![]() 中,求出函数解析式,再根据二次函数的性质求出最大值即可;
中,求出函数解析式,再根据二次函数的性质求出最大值即可;
(2)求出对称轴为直线![]() ,可知点
,可知点![]() 关于对称轴的对称点是
关于对称轴的对称点是![]() ,再根据图象判断出x的取值范围即可.
,再根据图象判断出x的取值范围即可.
解:(1)![]() 图象过点
图象过点![]() ,
,
![]() ,
,
解得![]()
![]() .
.
![]() .
.
![]() 的顶点坐标为
的顶点坐标为![]() .
.
![]() ,
,
∴当![]() 时,
时,![]() 最大=25.
最大=25.
答:该商品的销售单价为10元时,每天的销售利润最大,最大利润为25元.
(2)∵函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() ,
,
可知点![]() 关于对称轴的对称点是
关于对称轴的对称点是![]() ,
,
又∵函数![]() 图象开口向下,
图象开口向下,
∴当![]() 时,
时,![]() .
.
答:销售单价不少于8元且不超过12元时,该种商品每天的销售利润不低于21元.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
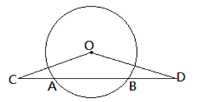
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).