题目内容
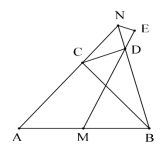
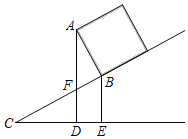
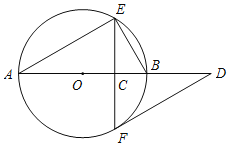
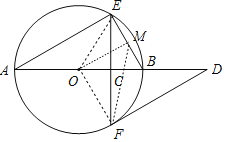
【题目】如图,AB是⊙O的直径,弦EF⊥AB于点C,过点F作⊙O的切线交AB的延长线于点D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中点M,连接MF,请补全图形;若∠A=30°,MF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)∠D=90°﹣2α;(2)⊙O的半径为2.
【解析】
(1)连接OE,OF,如图,利用等腰三角形的性质得到∠DOF=∠DOE.而∠DOE=2∠A,所以∠DOF=2α,再根据切线的性质得∠OFD=90°.从而得到∠D=90°﹣2α;
(2)连接OM,如图,利用圆周角定理得到∠AEB=90°.再证明OM∥AE得到∠MOB=∠A=30°.而∠DOF=2∠A=60°,所以∠MOF=90°,设⊙O的半径为r,利用含30度的直角三角形三边的关系得OM=![]() BM=
BM=![]() r,然后根据勾股定理得到即(
r,然后根据勾股定理得到即(![]() r)2+r2=(
r)2+r2=(![]() )2,再解方程即可得到⊙O的半径.
)2,再解方程即可得到⊙O的半径.
解:(1)连接OE,OF,如图,
∵EF⊥AB,AB是⊙O的直径,
∴∠DOF=∠DOE.
∵∠DOE=2∠A,∠A=α,
∴∠DOF=2α,
∵FD为⊙O的切线,
∴OF⊥FD.
∴∠OFD=90°.
∴∠D+∠DOF=90°,
∴∠D=90°﹣2α;
(2)连接OM,如图,
∵AB为⊙O的直径,
∴O为AB中点,∠AEB=90°.
∵M为BE的中点,
∴OM∥AE,
∵∠A=30°,
∴∠MOB=∠A=30°.
∵∠DOF=2∠A=60°,
∴∠MOF=90°,
设⊙O的半径为r,
在Rt△OMB中,BM=![]() OB=
OB=![]() r,
r,
OM=![]() BM=
BM=![]() r,
r,
在Rt△OMF中,OM2+OF2=MF2.
即(![]() r)2+r2=(
r)2+r2=(![]() )2,解得r=2,
)2,解得r=2,
即⊙O的半径为2.

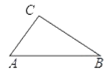
【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)