题目内容
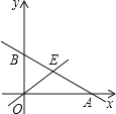
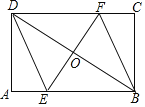
【题目】如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若AB=16cm,BC=8cm,求四边形DEBF的面积.
【答案】(1)详见解析;(2)80(cm2)
【解析】
(1)由题意得出∠OBE=∠ODF,由BD的垂直平分线得出OB=OD,证得△BOE≌△DOF,得出OE=OF,推出四边形BEDF是平行四边形,再由EF垂直平分BD,得出BE=DE,即可得出结论;
(2)由矩形、菱形的性质与勾股定理解得:BE=10cm,即可得出结果.
(1)证明:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC,AB∥DC,
∴∠OBE=∠ODF,
∵BD的垂直平分线分别交AB、CD、BD于E、F、O,
∴OB=OD,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(ASA),
∴OE=OF,
∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF垂直平分BD,
∴BE=DE,
∴四边形BEDF是菱形;
(2)解∵四边形ABCD是矩形,
∴AD=BC=8cm,AE=AB-BE=16-BE,
∵BE=DE,在Rt△DAE中,DE2=AD2+AE2,
即BE2=82+(16-BE)2,
解得:BE=10(cm),
∴四边形DEBF的面积=ADBE=8×10=80(cm2)

练习册系列答案
相关题目