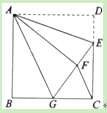
题目内容
【题目】已知:如图,![]() 中,
中,![]() 、
、![]() 两点分别是边
两点分别是边![]() 和
和![]() 的垂直平分线与
的垂直平分线与![]() 的交点,连结
的交点,连结![]() 和
和![]() ,且
,且![]() .求
.求![]() 的度数.
的度数.

证明:∵![]() 、
、![]() 两点分别是边
两点分别是边![]() 和
和![]() 的垂直平分线与
的垂直平分线与![]() 的交点,
的交点,
∴![]() ______________,
______________,![]() .( )
.( )
∵![]() ,
,
∴在![]() 中,
中,![]() ___________________(等量代换)
___________________(等量代换)
∴![]() 是____________三角形.
是____________三角形.
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ____________.
____________.
又∵![]() 的外角,
的外角,
∴![]() __________+∠___________
__________+∠___________![]() .
.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴![]() ____________.
____________.
【答案】见解析
【解析】
根据线段垂直平分线的性质得出PA=PB,QC=QA,再根据![]() 得出△APQ为等边三角形,再根据等腰三角形的性质和三角形的外角的性质求得∠C =30°,从而求解.
得出△APQ为等边三角形,再根据等腰三角形的性质和三角形的外角的性质求得∠C =30°,从而求解.
证明:∵![]() 、
、![]() 两点分别是边
两点分别是边![]() 和
和![]() 的垂直平分线与
的垂直平分线与![]() 的交点,
的交点,
∴![]() ____PB__,
____PB__,![]() .( 线段垂直平分线的性质)
.( 线段垂直平分线的性质)
∵![]() ,
,
∴在![]() 中,
中,![]() _AP=AQ_(等量代换)
_AP=AQ_(等量代换)
∴![]() 是___等边__三角形.
是___等边__三角形.
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() _QAC__.
_QAC__.
又∵![]() 是
是![]() 的外角,
的外角,
∴![]() __C________+∠__QAC_____
__C________+∠__QAC_____![]() .
.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴![]() _30°_.
_30°_.

练习册系列答案
相关题目