题目内容
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依次类推,若第![]() 次操作余下的四边形是菱形,则称原平行四边形为
次操作余下的四边形是菱形,则称原平行四边形为![]() 阶准菱形,如图1,□
阶准菱形,如图1,□![]() 为1阶准菱形.
为1阶准菱形.
(1)猜想与计算
邻边长分别为3和5的平行四边形是 阶准菱形;已知□![]() 的邻边长分别为
的邻边长分别为![]() (
(![]() ),满足
),满足![]() ,
,![]() ,请写出□
,请写出□![]() 是 阶准菱形.
是 阶准菱形.
(2)操作与推理
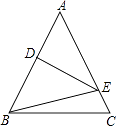
小明为了剪去一个菱形,进行如下操作:如图2,把□![]() 沿
沿![]() 折叠(点
折叠(点![]() 在
在![]() 上),使点
上),使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() .请证明四边形
.请证明四边形![]() 是菱形.
是菱形.
【答案】(1)3,12(2)证明见解析
【解析】
试题分析:(1)利用平行四边形准菱形的意义即可得出结论;
(2)先判断出∠AEB=∠ABE,进而判断出AE=BF,即可得出结论.
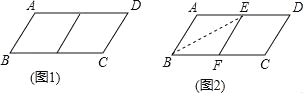
试题解析:(1)如图1,
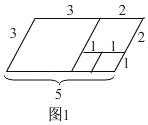
利用邻边长分别为3和5的平行四边形进行3次操作,所剩四边形是边长为1的菱形,
故邻边长分别为3和5的平行四边形是3阶准菱形:
如图2,
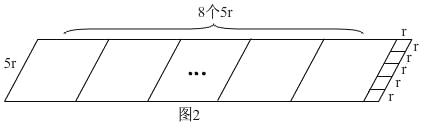
∵b=5r,
∴a=8b+r=40r+r=8×5r+r,
利用邻边长分别为41r和5r的平行四边形进行8+4=12次操作,所剩四边形是边长为1的菱形,
故邻边长分别为41r和5r的平行四边形是12阶准菱形:
故答案为:3,12
(2)由折叠知:∠ABE=∠FBE,AB=BF,
∵四边形ABCD是平行四边形,
∴AE∥BF,
∴∠AEB=∠FBE,
∴∠AEB=∠ABE,
∴AE=AB,
∴AE=BF,
∴四边形ABFE是平行四边形,
∴四边形ABFE是菱形

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】八年级5班的李军同学为了解他家所在小区居民的用电情况,随机对该小区20户居民进行了调查,下表是这20户小区居民2015年10月份用电量的调查结果:那么关于这20户小区居民月用电量(单位:度),下列说法正确的是( )
居民(户) | 2 | 6 | 4 | 8 |
月用电量(度/户) | 40 | 50 | 55 | 60 |
A.中位数是55
B.众数是8
C.方差是29
D.平均数是53.5