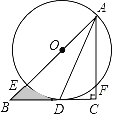
题目内容
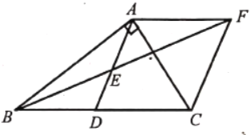
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)证明:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() ,直接写出菱形
,直接写出菱形![]() 的面积.
的面积.
【答案】(1)见解析;(2)见解析;(3)10
【解析】
(1)根据AAS证![]() AEF≌
AEF≌![]() DEB;
DEB;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,
∴AE=DE,BD=CD,
在![]() AFE和
AFE和![]() DBE中,
DBE中,
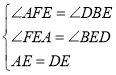 ,
,
∴![]() AFE≌
AFE≌![]() DBE(AAS);
DBE(AAS);
(2)证明:由(1)知,![]() AFE≌
AFE≌![]() DBE,
DBE,
则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
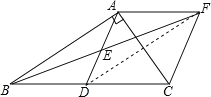
(3)解:连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=![]() ACDF
ACDF
=![]() ×4×5
×4×5
=10.

【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
【题目】在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共![]() 个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,下表是他们整理得到的试验数据:
摸球的次数 |
|
|
|
|
|
|
摸到红球的次数 |
|
|
|
|
|
|
摸到红球的频率 |
|
|
|
|
|
|
(1)试估计:盒子中有红球 个;
(2)若从盒子中一次性摸出两个球,用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率.