ЬтФПФкШн
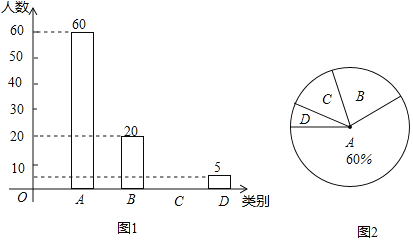
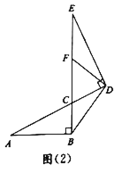
ЁОЬтФПЁПаЁУїНЋСНИіжБНЧШ§НЧаЮжНЦЌШчЭМЃЈ1ЃЉФЧбљЦДЗХдкЭЌвЛЦНУцЩЯЃЌГщЯѓГіШчЭМЃЈ2ЃЉЕФЦНУцЭМаЮЃЌ![]() гы
гы![]() ЧЁКУЮЊЖдЖЅНЧЃЌ
ЧЁКУЮЊЖдЖЅНЧЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЕуFЪЧЯпЖЮ
ЃЌЕуFЪЧЯпЖЮ![]() ЩЯвЛЕуЃЎ
ЩЯвЛЕуЃЎ
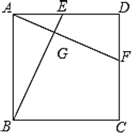
ЬНОПЗЂЯжЃК
ЃЈ1ЃЉЕБЕуFЮЊЯпЖЮ![]() ЕФжаЕуЪБЃЌСЌНг
ЕФжаЕуЪБЃЌСЌНг![]() ЃЈШчЭМЃЈ2ЃЉЃЌаЁУїОЙ§ЬНОПЃЌЕУЕННсТлЃК
ЃЈШчЭМЃЈ2ЃЉЃЌаЁУїОЙ§ЬНОПЃЌЕУЕННсТлЃК![]() ЃЎФуШЯЮЊДЫНсТлЪЧЗёГЩСЂЃП_________ЃЎЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉ
ЃЎФуШЯЮЊДЫНсТлЪЧЗёГЩСЂЃП_________ЃЎЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉ
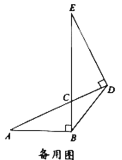
ЭиеЙбгЩьЃК
ЃЈ2ЃЉНЋЃЈ1ЃЉжаЕФЬѕМўгыНсТлЛЅЛЛЃЌМДЃКШє![]() ЃЌдђЕуFЮЊЯпЖЮ
ЃЌдђЕуFЮЊЯпЖЮ![]() ЕФжаЕуЃЎЧыХаЖЯДЫНсТлЪЧЗёГЩСЂЃЎШєГЩСЂЃЌЧыаДГіжЄУїЙ§ГЬЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЕФжаЕуЃЎЧыХаЖЯДЫНсТлЪЧЗёГЩСЂЃЎШєГЩСЂЃЌЧыаДГіжЄУїЙ§ГЬЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЮЪЬтНтОіЃК
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЪЧЃЛЃЈ2ЃЉНсТлГЩСЂЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
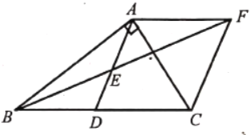
ЃЈ1ЃЉРћгУЕШНЧЕФгрНЧЯрЕШЧѓГіЁЯA=ЁЯEЃЌдйЭЈЙ§AB=BDЧѓГіЁЯA=ЁЯADBЃЌНєНгзХИљОнжБНЧШ§НЧаЮаББпЕФжаЯпЕШгкаББпЕФвЛАыЧѓГіFD=FE=FCЃЌгЩДЫЕУГіЁЯE=ЁЯFDEЃЌОнДЫНјвЛВНЕУГіЁЯADB=ЁЯFDEЃЌзюжеЭЈЙ§жЄУїЁЯADB+ЁЯEDC=90ЁужЄУїНсТлГЩСЂМДПЩЃЛ
ЃЈ2ЃЉИљОнДЙжБЕФаджЪПЩвдЕУГі![]() 90ЁуЃЌ
90ЁуЃЌ![]() 90ЁуЃЌДгЖјПЩЕУ
90ЁуЃЌДгЖјПЩЕУ![]() ЃЌНгзХжЄУїГі
ЃЌНгзХжЄУїГі![]() ЃЌРћгУ
ЃЌРћгУ![]() ПЩжЊ
ПЩжЊ![]() ЃЌДгЖјЭЦГі
ЃЌДгЖјЭЦГі![]() ЃЌзюКѓЭЈЙ§жЄУї
ЃЌзюКѓЭЈЙ§жЄУї![]() ЕУГі
ЕУГі![]() ЃЌОнДЫМгвдЗжЮіМДПЩжЄУїНсТлЃЛ
ЃЌОнДЫМгвдЗжЮіМДПЩжЄУїНсТлЃЛ
ЃЈ3ЃЉШчЭМЃЌЩшGЮЊ![]() ЕФжаЕуЃЌСЌНгGDЃЌгЩЃЈ1ЃЉЕУ
ЕФжаЕуЃЌСЌНгGDЃЌгЩЃЈ1ЃЉЕУ![]() ЃЌЙЪЖј
ЃЌЙЪЖј![]() ЃЌдк
ЃЌдк![]() жаЃЌРћгУЙДЙЩЖЈРэЧѓГі
жаЃЌРћгУЙДЙЩЖЈРэЧѓГі![]() ЃЌгЩДЫЕУГі
ЃЌгЩДЫЕУГі![]() ЃЌНєНгзХЃЌМЬајЭЈЙ§ЙДЙЩЖЈРэЧѓГі
ЃЌНєНгзХЃЌМЬајЭЈЙ§ЙДЙЩЖЈРэЧѓГі![]() ЃЌзюКѓНјвЛВНжЄУї
ЃЌзюКѓНјвЛВНжЄУї![]() ЃЌдйИљОнЯрЫЦШ§НЧаЮаджЪЕУГі
ЃЌдйИљОнЯрЫЦШ§НЧаЮаджЪЕУГі![]() ЃЌДгЖјЧѓГі
ЃЌДгЖјЧѓГі![]() ЃЌзюКѓНјвЛВНЗжЮіЧѓНтМДПЩ.
ЃЌзюКѓНјвЛВНЗжЮіЧѓНтМДПЩ.
ЃЈ1ЃЉЁпЁЯABC=ЁЯCDE=90ЁуЃЌ
ЁрЁЯA+ЁЯACB=ЁЯE+ЁЯECDЃЌ
ЁпЁЯACB=ЁЯECDЃЌ
ЁрЁЯA=ЁЯEЃЌ
ЁпAB=BDЃЌ
ЁрЁЯA=ЁЯADBЃЌ
дк![]() жаЃЌ
жаЃЌ
ЁпFЪЧаББпCEЕФжаЕуЃЌ
ЁрFD=FE=FCЃЌ
ЁрЁЯE=ЁЯFDEЃЌ
ЁпЁЯA=ЁЯEЃЌ
ЁрЁЯADB=ЁЯFDEЃЌ
ЁпЁЯFDE+ЁЯFDC=90ЁуЃЌ
ЁрЁЯADB+ЁЯFDC=90ЁуЃЌ
МДЁЯFDB=90ЁуЃЌ
ЁрBDЁЭDFЃЌНсТлГЩСЂЃЌ
ЙЪД№АИЮЊЃКЪЧЃЛ
ЃЈ2ЃЉНсТлГЩСЂЃЌРэгЩШчЯТЃК
Ёп![]() ЃЌ
ЃЌ![]()
Ёр![]() 90ЁуЃЌ
90ЁуЃЌ![]() 90ЁуЃЌ
90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
гж![]() 90ЁуЃЌ
90ЁуЃЌ![]() 90ЁуЃЌ
90ЁуЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрFЮЊ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈ3ЃЉШчЭМЃЌЩшGЮЊ![]() ЕФжаЕуЃЌСЌНгGDЃЌгЩЃЈ1ЃЉПЩжЊ
ЕФжаЕуЃЌСЌНгGDЃЌгЩЃЈ1ЃЉПЩжЊ![]() ЃЌ
ЃЌ
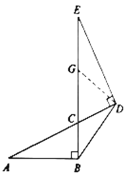
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ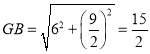 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
дк![]() гы
гы![]() жаЃЌ
жаЃЌ
ЁпЁЯABC=ЁЯEDCЃЌЁЯACB=ЁЯECDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ

 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЪЧГЃЪ§ЃЌ
ЪЧГЃЪ§ЃЌ![]() ЃЉЕФ
ЃЉЕФ![]() гы
гы![]() ЕФВПЗжЖдгІжЕШчЯТБэЃК
ЕФВПЗжЖдгІжЕШчЯТБэЃК
|
|
|
| 0 | 2 |
| 6 | 0 |
|
| 6 |
ЯТСаНсТлЃК
Ђй![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌКЏЪ§зюаЁжЕЮЊ
ЪБЃЌКЏЪ§зюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЂлШєЕу![]() ЃЌЕу
ЃЌЕу![]() дкЖўДЮКЏЪ§ЭМЯѓЩЯЃЌдђ
дкЖўДЮКЏЪ§ЭМЯѓЩЯЃЌдђ![]() ЃЛ
ЃЛ
ЂмЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЦфжаЃЌе§ШЗНсТлЕФађКХЪЧ__________________ЃЎЃЈАбЫљгае§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮABCDЮЊОиаЮЃЌЧњЯпLОЙ§ЕуDЃЎЕуQЪЧЫФБпаЮABCDФквЛЖЈЕуЃЌЕуPЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌзїPMЁЭABНЛЧњЯпLгкЕуMЃЌСЌНгQMЃЎ
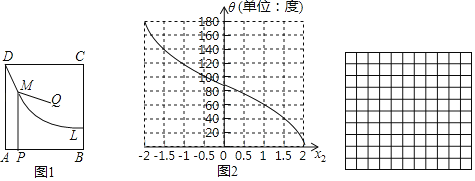
аЁЖЋЭЌбЇЗЂЯжЃКдкЕуPгЩAдЫЖЏЕНBЕФЙ§ГЬжаЃЌЖдгкx1ЃНAPЕФУПвЛИіШЗЖЈЕФжЕЃЌІШЃНЁЯQMPЖМгаЮЈвЛШЗЖЈЕФжЕгыЦфЖдгІЃЌx1гыІШЕФЖдгІЙиЯЕШчБэЫљЪОЃК
x1ЃНAP | 0 | 1 | 2 | 3 | 4 | 5 |
ІШЃНЁЯQMP | ІС | 85Ёу | 130Ёу | 180Ёу | 145Ёу | 130Ёу |
аЁмПЭЌбЇдкЖСЪщЪБЃЌЗЂЯжСЫСэЭтвЛИіКЏЪ§ЃКЖдгкздБфСПx2дкЉ2Ёмx2Ём2ЗЖЮЇФкЕФУПвЛИіжЕЃЌЖМгаЮЈвЛШЗЖЈЕФНЧЖШІШгыжЎЖдгІЃЌx2гыІШЕФЖдгІЙиЯЕШчЭМ2ЫљЪОЃК
ИљОнвдЩЯВФСЯЃЌЛиД№ЮЪЬтЃК
ЃЈ1ЃЉБэИёжаІСЕФжЕЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЙћСюБэИёжаx1ЫљЖдгІЕФІШЕФжЕгыЭМ2жаx2ЫљЖдгІЕФІШЕФжЕЯрЕШЃЌПЩвддкСНИіБфСПx1гыx2жЎМфНЈСЂКЏЪ§ЙиЯЕЃЎ
ЂйдкетИіКЏЪ§ЙиЯЕжаЃЌздБфСПЪЧЁЁ ЃЌвђБфСПЪЧЁЁ ЃЛЃЈЗжБ№ЬюШыx1КЭx2ЃЉ
ЂкЧыдкЭјИёжаНЈСЂЦНУцжБНЧзјБъЯЕЃЌВЂЛГіетИіКЏЪ§ЕФЭМЯѓЃЛ
ЂлИљОнЛГіЕФКЏЪ§ЭМЯѓЃЌЕБAPЃН3.5ЪБЃЌx2ЕФжЕдМЮЊЁЁ ЃЎ