题目内容
【题目】如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积 . 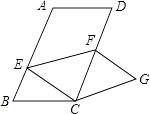
【答案】![]()
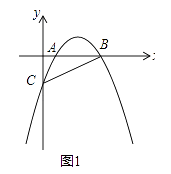
【解析】解:如图1,作CK⊥AB于K,过E点作EP⊥BC于P. 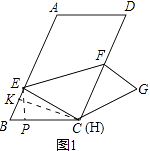
∵∠B=60°,
∴CK=BCsin60°=4× ![]() =2
=2 ![]() ,
,
∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离,
∴点E到CD的距离是2 ![]() ,
,
∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,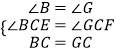 ,
,
∴△BCE≌△GCF(ASA);
∴CE=CF,
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BEsin60°=2m× ![]() =
= ![]() m,
m,
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6﹣2m,
∵BC=4,
∴PC=4﹣m,
在Rt△ECP中,由勾股定理得(4﹣m)2+( ![]() ﹣m)2=(6﹣2m)2 , 解得m=
﹣m)2=(6﹣2m)2 , 解得m= ![]() ,
,
∴EC=6﹣2m=6﹣2× ![]() =
= ![]() ,
,
∴CF=EC= ![]() ,
,
∴S△CEF= ![]() ×
× ![]() ×2
×2 ![]() =
= ![]() ,
,
故答案为 ![]() .
.
如图1,作CK⊥AB于K,过E点作EP⊥BC于P.想办法求出CK、EP、EC,再证明△BCE≌△GCF(ASA)推出CE=CF,根据三角形的面积公式计算即可.

练习册系列答案
相关题目