题目内容
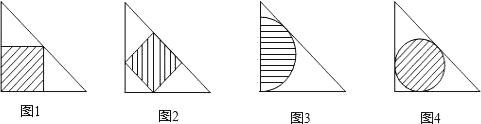
【题目】如图，甲、乙、丙、丁四位同学从四块全等的等腰直角三角形纸板上裁下四块不同的纸板（阴影部分），他们的具体裁法如下：甲同学：如图1所示裁下一个正方形，面积记为S1；乙同学：如图2所示裁下一个正方形，面积记为S2；丙同学：如图3所示裁下一个半圆，使半圆的直径在等腰Rt△的直角边上，面积记为S3；丁同学：如图所示裁下一个内切圆，面积记为S4则下列判断正确的是（ ）
①S1=S2；②S3=S4；③在S1，S2，S3，S4中，S2最小．
A. ①② B. ②③ C. ①③ D. ①②③
【答案】B
【解析】分析：分别计算结果再比较大小．具体如下：若设四块全等的等腰直角三角形的腰长为1，则斜边长为
，只要把四个图中阴影部分的面积都用等腰直角三角形的腰长表示，就可比较它们的大小．根据直角三角形中斜边上的中线等于斜边的一半，可求图1中S1=
；设图2中正方形的边长为x，根据等腰直角三角形的性质求得x的值，所以可知S2=
；在图3中，设半圆的半径为r，根据切线长定理可求得S3=（
﹣）π；在图4中，设三角形的内切圆半径为R，根据切线长定理可求得R=1﹣
，所以S4=（
）π；根据以上计算的值进行比较即可判断．
详解：图1中，设四块全等的等腰直角三角形的腰长为1，则斜边长为，图1中阴影正方形的对角线长为，S1=；
图2中，设正方形的边长为x，则3x=，x=
，S2=；
图3中，设半圆的半径为r，则1+r=，r=﹣1，S3=（﹣）π；
图4中，设三角形的内切圆半径为R，则2﹣2R=，解得：R=1﹣，S4=（）π；
根据以上计算的值进行比较，S3=S4，在S1，S2，S3，S4中，S2最小，所以正确的是②③．
故选B．
练习册系列答案
相关题目
