题目内容
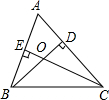
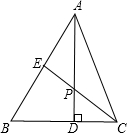
如图,△ABC中AD是BC边上的高,CE是△ABC的一条角平分线,它们相交于点P.已知∠APE=55°,
∠AEP=75°,求△ABC的各个内角的度数.
∠AEP=75°,求△ABC的各个内角的度数.

∵∠APE=55°,∠AEP=75°,
∴∠BAD=180°-55°-75°=50°.
∵AD⊥BC,
∴∠B=90°-50°=40°,
∴∠BCE=∠AEC-∠B=75°-40°=35°.
又CE平分∠ACB,
∴∠ACB=70°,
∴∠BAC=180°-∠B-∠ACB=70°.
∴∠BAD=180°-55°-75°=50°.
∵AD⊥BC,
∴∠B=90°-50°=40°,
∴∠BCE=∠AEC-∠B=75°-40°=35°.
又CE平分∠ACB,
∴∠ACB=70°,
∴∠BAC=180°-∠B-∠ACB=70°.

练习册系列答案
相关题目