题目内容
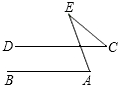
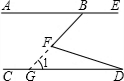
如图，直线AE∥CD，∠EBF=135°，∠BFD=60°，则∠D等于（ ）
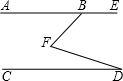
| A．75° | B．45° | C．30° | D．15° |
延长BF交CD于G点，如图
∵AE∥CD，∠EBF=135°（已知）
∴∠1=180°-∠EBF=180°-135°=45°（两直线平行，同旁内角互补）．
又∵∠BFD=∠1+∠D（三角形外角的性质），
∴∠D=∠BFD-∠1=60°-45°=15°．
故选D．
∵AE∥CD，∠EBF=135°（已知）
∴∠1=180°-∠EBF=180°-135°=45°（两直线平行，同旁内角互补）．
又∵∠BFD=∠1+∠D（三角形外角的性质），
∴∠D=∠BFD-∠1=60°-45°=15°．
故选D．
练习册系列答案
字词句段篇系列答案
相关题目
