题目内容
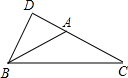
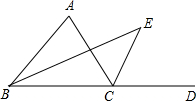
如图,在△ABC中,BE是∠ABC的内角平分线,CE是∠ACB的外角平分线,BE、CE交于E点,试探究∠E与∠A的大小关系.

∠E=
∠A
证明:∵∠ACD=∠A+∠ABC,CE平分∠ACD,
∴∠ECD=
∠ACD=
(∠A+∠ABC)(角平分线的定义),
∵BE平分∠ABC,
∴∠EBC=
∠ABC(角平分线的定义),
∵∠ECD是△BCE的外角,
∴∠E=∠ECD-∠EBC=
∠A.
| 1 |
| 2 |
证明:∵∠ACD=∠A+∠ABC,CE平分∠ACD,
∴∠ECD=
| 1 |
| 2 |
| 1 |
| 2 |
∵BE平分∠ABC,
∴∠EBC=
| 1 |
| 2 |
∵∠ECD是△BCE的外角,
∴∠E=∠ECD-∠EBC=
| 1 |
| 2 |

练习册系列答案
相关题目