题目内容
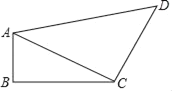
【题目】如图①,直角三角形ABC中,∠B=90°.将它放在平面直角坐标系中,A(0,1),且满足(AB-4)2+![]() =0.
=0.
(1)求直线AC的解析式.
(2)在直线BC上是否存在点P,使S△APC= 6?若存在,求P点坐标;若不存在,说明理由.
(3)如果M在y轴上,且△AMC是以AC为腰的等腰三角形,求M的坐标
(4)如果D是AC的中点,问在y轴上是否存在点M,使得MD+ ![]() AC最小?存在的话,请直接写出M的坐标。
AC最小?存在的话,请直接写出M的坐标。

【答案】(1)y=0.5x+1;(2)P(4,0)(4,6);(3)![]()
![]()
![]() ;(4)
;(4)![]() .
.
【解析】
试题![]() 由
由![]() 求得
求得![]() 的值,进而求得点
的值,进而求得点![]() 的坐标,求得直线
的坐标,求得直线![]() 的解析式.
的解析式.
![]() 由
由![]() 求得
求得![]() 的长度,进而确定点
的长度,进而确定点![]() 的坐标.
的坐标.
![]() 设点
设点![]() ,根据等腰三角形的性质,即可求得点
,根据等腰三角形的性质,即可求得点![]() 的坐标.
的坐标.
![]() 作点
作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 即为所求.
即为所求.
试题解析:试题![]() 由
由![]()
则![]()
![]()
由图可得点![]()
设直线![]() 的解析式为:
的解析式为:![]()
![]()
解得:![]()
直线![]() 的解析式为:
的解析式为:![]()
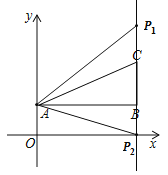
![]() 如图所示:
如图所示:
由![]()
解得:![]()
点![]() 在直线
在直线![]() 上,
上,
点![]() 的坐标为:
的坐标为:![]() 或
或![]()
![]() 设点
设点![]() ,根据等腰三角形的性质,
,根据等腰三角形的性质,![]() 或
或![]()
当![]() 时,
时,![]()
![]()
![]()
![]() 或
或![]()
当![]() 时,
时,![]()
![]() 如图所示:
如图所示:
作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 即为所求.
即为所求.
![]()


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目