题目内容
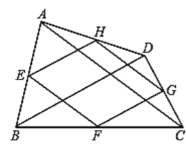
【题目】如图，点
、
、
、
分别是四边形
边
、
、
、
的中点，则下列说法：
①若
，则四边形
为矩形；
②若
，则四边形为菱形；
③若四边形是平行四边形，则
与
互相垂直平分；
④若四边形是正方形，则与互相垂直且相等.
其中正确的个数是（ ）
A.1B.2C.3D.4
【答案】A
【解析】
根据三角形中位线定理、平行四边形的判定定理得到四边形EFGH是平行四边形，根据矩形、菱形、正方形的判定定理判断即可．
解：∵E、F分别是边AB、BC的中点，
∴EF∥AC，EF=
AC，
同理可知，HG∥AC，HG=AC，
∴EF∥HG，EF=HG，
∴四边形EFGH是平行四边形，
若AC=BD，则四边形EFGH是菱形，故①说法错误；
若AC⊥BD，则四边形EFGH是矩形，故②说法错误；
若四边形
是平行四边形，AC与BD不一定互相垂直平分，故③说法错误；
若四边形是正方形，AC与BD互相垂直且相等，故④说法正确；
故选：A．
【题目】某学校在开展“节约每一滴水”的活动中，从七年级的100名同学中选出20名同学汇报了各自家庭一个月的节水情况，将有关数据（每人上报节水量都是正整数）整理如下表：
节水量x/t | 0.5≤x＜1.5 | 1.5≤x＜2.5 | 2.5≤x＜3.5 | 3.5≤x＜4.5 |
人数 | 6 | 4 | 8 | 2 |
请你估计这100名同学的家庭一个月节约用水的总量大约是（ ）
A.180tB.300tC.230tD.250t
【题目】养牛场的李大叔分三次购进若干头大牛和小牛．其中有一次购买大牛和小牛的价格同时打折，其余两次均按原价购买，三次购买的数量和总价如下表：
（1）李大叔以折扣价购买大牛和小牛是第 次；是打 折.
（2）用解方程（组）的方法求大牛和小牛的原价.
大牛（头） | 小牛（头） | 总价（元） | |
第一次 | 4 | 3 | 9900 |
第二次 | 2 | 6 | 9000 |
第三次 | 6 | 9 | 13230 |
【题目】某自行车厂计划每天生产
辆自行车，但由于各种原因，实际每天生产量与计划生产量相比有所差异，下表是该厂某一周的实际生产情况（以计划产量为标准，超产记为正数，不足记为负数．单位：辆）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与标准产量的差 |
|
|
|
|
|
|
|
（
）根据表格，这一周该厂实际生产自行车多少辆？
（
）若该厂实行“每日计件工资制”，每生产一辆自行车可得
元，若超额完成任务，则超出部分每辆额外奖励
元；若未完成任务，则每少生产一辆扣
元，那么该厂工人这一周的工资总额是多少元？
（
）若将（）中的“每日计件工资制”改为“每周计件工资制”，其他条件不变，在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了？减少或增加了多少？
