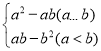题目内容
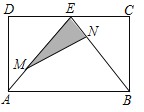
【题目】如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图像为( )
A. 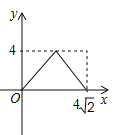 B.
B. 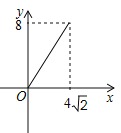
C. 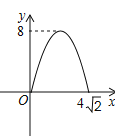 D.
D. 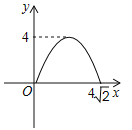
【答案】D
【解析】
证明△ABE是等腰直角三角形,连接MB,利用等高模型表示出△EMN,△EBM,△EAB之间的关系即可解决问题.
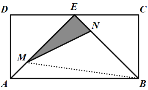
如图,连接MB,
∵E为DC中点,
∴DE=CE=4,
∴AD=DE=CD=BC=4,
∵四边形ABCD是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△EAB是等腰直角三角形,
由勾股定理AE=BE=![]() ,
,
已知,AM=t,EN=t,ME=NB=![]() ,
,
∵S△EMN∶S△EMB=EN∶EB,
∴S△EMN=![]() ,
,
∵S△EMB∶S△EAB=EM∶EA,
∴S△EMB=![]() ,
,
∴S=![]() ,
,
∵a=![]() <0,
<0,
∴当t=![]() 时,S的最大值为4.
时,S的最大值为4.
故选:D.

练习册系列答案
相关题目