题目内容
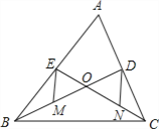
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC. 
(1)猜测AE与BE的数量关系,并说明理由;
(2)求证:四边形AEDF是菱形.
【答案】
(1)解:AE= ![]() BE.理由如下:
BE.理由如下:
Rt△ABC中,∠A=60°,得∠B=30°.
则在Rt△BDE中有DE= ![]() BE.
BE.
由对折可知AE=DE,则AE= ![]() BE
BE
(2)证明:由∠C=90°,ED⊥BC得DE∥AC,
∴∠DFC=∠EDF=∠A=60°,
∴DF∥AE.
∴四边形AEDF是平行四边形.
又AE=ED,
∴平行四边形AEDF是菱形
【解析】(1)在Rt△ABC中,由直角三角形的性质:两锐角互余得∠B=30°,则在Rt△ADE中有DE=BEsin30°= ![]() BE,又由对折可知AE=DE,则AE=
BE,又由对折可知AE=DE,则AE= ![]() BE;(2)易得DE∥AC,所以∠DFC=∠EDF=∠A=60°,所以DF∥AE. 由两组对边分别平行的四边形是平行四边形得,四边形AEDF是平行四边形.
BE;(2)易得DE∥AC,所以∠DFC=∠EDF=∠A=60°,所以DF∥AE. 由两组对边分别平行的四边形是平行四边形得,四边形AEDF是平行四边形.
又AE=ED,所以邻边相等的平行四边形AEDF是菱形.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目