题目内容
【题目】已知：∠1＝∠2，EG 平分∠AEC．
(1)如图1，∠MAE＝50°，∠FEG＝15°，∠NCE＝80°．试判断 EF 与 CD 的位置关系，并说明理由．
(2)如图2，∠MAE＝135°，∠FEG＝30°，当 AB∥CD 时，求∠NCE 的度数；
(3)如图2，试写出∠MAE、∠FEG、∠NCE 之间满足什么关系时，AB∥CD．
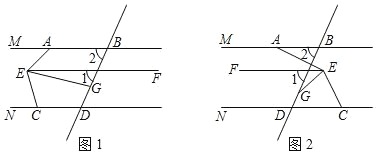
【答案】（1）
，证明见解析 （2）75° （3）
，证明见解析
【解析】
（1）根据
可得
，根据角的和差关系和角平分线的性质可得
，从而得证；
（2）根据可得，根据平行线的性质以及角平分线的性质可得
；
（3）根据可得，根据平行线的性质可得
，再根据角平分线的性质可得
，再根据平行线的性质即可得．
（1）
∵
∴
∴
∴
∵EG 平分∠AEC
∴
∴
∴
∴；
（2）∵
∴
∵∠MAE
∴
∵∠FEG＝30°
∴
∵EG 平分∠AEC
∴
∵
∴；
（3）
∵
∴
∴
∴
∴
∵EG 平分∠AEC
∴
∴
∴
∴
∵
∴
∴
∴
∴．
练习册系列答案
名校课堂系列答案
相关题目
