题目内容
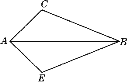
【题目】某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是cm. 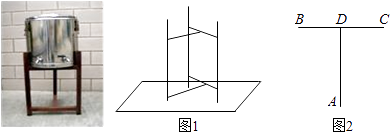
【答案】30
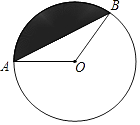
【解析】解:连接OB,如图,
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大.
∵AD垂直平分BC,AD=BC=48cm,
∴O点在AD上,BD=24cm;
在Rt△0BD中,设半径为r,则OB=r,OD=48﹣r,
∴r2=(48﹣r)2+242 , 解得r=30.
即圆柱形饮水桶的底面半径的最大值为30cm.
所以答案是:30.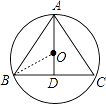
【考点精析】本题主要考查了勾股定理的概念和垂径定理的推论的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等才能正确解答此题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目