题目内容
【题目】如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
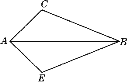
【答案】(1)见解析;(2)BC=BE.
【解析】
(1)根据作三角形的高的方法,作出AD、AF;
(2)根据HL证明Rt△ACD≌Rt△AEF,从而得出CD=EF,再根据HL证明Rt△ABD≌Rt△ABF,从而得出BD=BF,再利用等式的性质得出:BD-CD=BF-EF,即BC=BE.
解:(1)画出高AD,AF,如图所示.
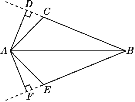
(2)猜想:BC=BE.证明如下:
∵AD⊥BC,AF⊥BE,
∴△ACD,△AEF,△ABD,△ABF都是直角三角形.
在Rt△ACD和Rt△AEF中,
![]()
∴Rt△ACD≌Rt△AEF(HL).
∴CD=EF(全等三角形的对应边相等).
在Rt△ABD和Rt△ABF中,
![]()
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF(全等三角形的对应边相等).
∴BD-CD=BF-EF(等式的性质),即BC=BE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目