题目内容
【题目】如图,直线![]() 交x轴于点A,交直线
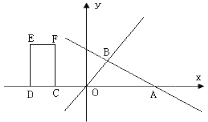
交x轴于点A,交直线![]() 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
(1)求b、m的值;
(2)当矩形CDEF运动t秒时,请直接写出C、D两点的坐标(用含t的代数式表示)
(3)当点B在矩形CDEF的一边上时,求t的值;
(4)设CF、DE分别交折线OBA于M、N两点,当四边形MCDN为直角梯形时,求t的取值范围.
【答案】(1)b=4,m=3;(2)点C(2t![]() 2,0)、点D(2t
2,0)、点D(2t![]() 4,0);(3)当点B在矩形的一边上时,t的值为2秒或3秒;(4)t的取值范围为:2<t<5且t≠
4,0);(3)当点B在矩形的一边上时,t的值为2秒或3秒;(4)t的取值范围为:2<t<5且t≠![]() .
.
【解析】
(1)把B点坐标分别代入![]() 和
和![]() 可求出m,b.
可求出m,b.
(2)C点向右移动2t个单位,则C点的横坐标要减2t,便可写出C,D两点坐标.
(3)首先判断B点在EF的下方,再讨论B点在DE或FC上,利用横坐标相等求t.
(4)通过端点确定范围,即C点到达A点,D点到达O点,还要去掉CM=DN时的t的值.
解:(1)把B(2,m)代入![]() ,得m=3.
,得m=3.
再把B(2,3)代入![]() ,得b=4.
,得b=4.
(2)因为点C向右移了2t个单位,则点C的横坐标加2t,纵坐标还是0,
D点的横坐标比点C要小2,
∴点C(2t-2,0)、点D(2t-4,0);
(3)∵3<4,
∴点B在EF的下方,不能在EF上,
点B在CF边上时2t-2=2,解得:t=2,
点B在DE边上时,2t-4=2,解得:t=3,
∴当点B在矩形的一边上时,t的值为2秒或3秒;
(4)点D与O重合时,2t-4=0,解得:t=2,
点C与点A重合时,2t-2=8,解得t=5,
CF交AB于M,DE交BO于N时,M(2t-2,5-t),N(2t-4,3t-6),
当CM=DN时,即5-t=3t-6,
解得t=![]() ,
,
∴当t=![]() 时四边形MCDN为矩形,
时四边形MCDN为矩形,
∴当四边形MCDN为直角梯形时,
t的取值范围为:2<t<5且t≠![]() .
.

 阅读快车系列答案
阅读快车系列答案