题目内容
【题目】在△ABC中,AB=AC,BC=12,E为边AC的中点,
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

【答案】(1)3(2)5(3)①![]() ②
②![]()
【解析】试题分析:(1)点A作AG⊥BC交BC于点G,则EH∥AG,由等腰三角形的性质得CG=6,再由E为AC中点可得H为CG的中点.
(2)①过点E作![]() 于点H,设
于点H,设![]() ,在Rt△EDH中可得
,在Rt△EDH中可得![]() ,解方程求出x的值;由
,解方程求出x的值;由![]()
![]() ,可得
,可得![]() ,
, ![]() ,在
,在![]() 中,根据勾股定理列出关系式
中,根据勾股定理列出关系式![]() ,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
解:(1)点A作AG⊥BC交BC于点G.
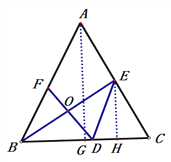
∵![]() ,
,
∴![]() ,
,
∵E为AC中点,EH∥AG,
∴H为CG的中点,∴CH=3,
⑵①过点E作![]() 于点H,
于点H,
∵△ABC是等腰直角三角形,则CH=EH=3,
设![]() ,则
,则![]() ,
, ![]() ,
,
Rt△EDH中, ![]() ,
,
解之得, ![]() ,
,
即BD=5,
②∵![]()
![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中,
![]() ,
,
∴![]() ,
,
方法一:由![]() 得,
得, ![]() ,
,
当y有最大值时,x有最大值.即tan∠ACB有最大值.
∴当y=12时, ![]() ,
, ![]() (负的舍去),
(负的舍去),
∴tan∠ACB最大值为![]() ,
,
或方法二:当点D与点C重合时,tan∠ACB最大,
![]() ,
,
![]() .
.
BC边的高为![]() ,
,
此时tan∠ACB=![]() .
.

练习册系列答案
相关题目