题目内容

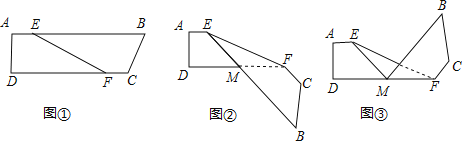
【题目】如图，图①是一个四边形纸条 ABCD，其中 AB∥CD，E，F 分别为边 AB，CD 上的两个点，将纸条 ABCD 沿 EF 折叠得到图②，再将图②沿 DF 折叠得到图③，若在图③中，∠FEM=26°，则∠EFC 的度数为（ ）

A.52°B.64°C.102°D.128°

【答案】C

【解析】

先由折叠得：∠BEF=2∠FEM=52°，由平行线的性质得∠EFM=26°，如图③中，根据折叠和平行线的性质得，∠MFC=128°，根据角的差可得结论．

如图①，由折叠得：∠BEF=2×26°=52°，

如图②，∵AE∥DF，

∴∠EFM=26°，∠BMF=∠DME=52°，

∵BM∥CF，

∴∠CFM+∠BMF=180°，

∴∠CFM=180°-52°=128°，

由折叠得：如图③，∠MFC=128°，

∴∠EFC=∠MFC-∠EFM=128°-26°=102°，

故选C．

练习册系列答案
相关题目

【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有90公里，队伍8：00从学校出发．苏老师因有事情，8：30从学校自驾小车以大巴1.5倍的速度追赶，追上大巴后继续前行，结果比队伍提前15分钟到达基地．问：

（1）大巴与小车的平均速度各是多少？

（2）苏老师追上大巴的地点到基地的路程有多远？

【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌

粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

（1）试求出每天的销售量y（盒）与每盒售价 （元）之间的函数关系式；（4分）

（2）当每盒售价定为多少元时，每天销售的利润 （元）最大？最大利润是多少？（6分）

【题目】如图，直线交x轴于点A，交直线于点B（2，m）．矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴的上方，DC=2，DE=4．当点C的坐标为（－2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．（注：矩形就是长方形）

（1）求b、m的值；

（2）当矩形CDEF运动t秒时，请直接写出C、D两点的坐标（用含t的代数式表示）

（3）当点B在矩形CDEF的一边上时，求t的值；

（4）设CF、DE分别交折线OBA于M、N两点，当四边形MCDN为直角梯形时，求t的取值范围．

【题目】如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）

A. 40° B. 45° C. 60° D. 70°

【题目】填空完成推理过程：

如图，∠1=∠2，∠A=∠D， 求证：∠B=∠C.

证明：∵∠1=∠2（已知），

∠1=∠3（ ），

∴∠2=∠3（等量代换）.

∴AF∥________（ ）.

∴∠D=∠4（两直线平行，同位角相等 ）.

∵∠A=∠D（已知），

∴∠A=∠4（等量代换）.

∴AB∥CD（内错角相等，两直线平行）.

∴∠B=∠C（ ）.

【题目】实验初中组织了“英语手抄报”征集活动，现从中随机抽取部分作品，按A、B、C、D四个等级进行评价，并根据统计结果绘制了如下两幅不完整的统计图．

（1）抽取了＿＿＿＿＿份作品；

（2）此次抽取的作品中等级为B的作品有＿＿＿＿＿＿份，并补全条形统计图；

（3）若该校共征集到600份作品，请估计等级为A的作品约有多少份？

【题目】如图是一个运算流程．

例如：根据所给的运算流程可知，当 x=5 时，5×3﹣1=14＜32，把 x=14 带入，14×3﹣1=41＞32，则输出值为 41．

（1）填空：当 x=15 时，输出值为__________；当 x=6 时，输出值为__________-；

（2）若需要经过两次运算，才能运算出 y，求 x 的取值范围．

【题目】某中学开展“阳光体育一小时”活动，按学校实际情况，决定开设A：踢毽子；B：篮球；C：跳绳；D：乒乓球四种运动项目，为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，井将调查结果绘制成如下两个统计图．请结合图中的信息解答下列问题．

（1）在扇形统计图中，“B”所在扇形的圆心角是多少度？；

（2）将条形统计图补充完整；

（3）若该中学有1200名学生，喜欢篮球运动的学生约有多少名？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网